Star Delta transformation

Star Delta transformation:

Star to Delta transformation:

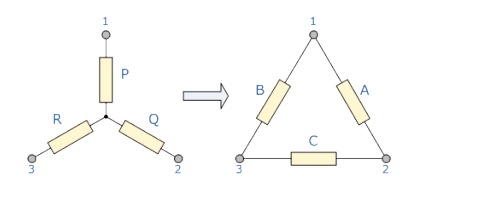
Star Delta Transformations allow us to convert impedances connected together from one type of connection to another. We can now solve simple series, parallel or bridge type resistive networks using Kirchhoff´s Circuit Laws, mesh current analysis or nodal voltage analysis techniques but in a balanced 3-phase circuit we can use different mathematical techniques to simplify the analysis of the circuit and thereby reduce the amount of math’s involved which in itself is a good thing.

Standard 3-phase circuits or networks take on two major forms with names that represent the way in which the resistances are connected, a Star connected network which has the symbol of the letter, Υ (wye) and a Delta connected network which has the symbol of a triangle, (delta).

If a 3-phase, 3-wire supply or even a 3-phase load is connected in one type of configuration, it can be easily transformed or changed it into an equivalent configuration of the other type by using either the Star Delta Transformation or Delta Star Transformation process.

A resistive network consisting of three impedances can be connected together to form a T or “Tee” configuration but the network can also be redrawn to form a Star or Υ type network as shown below.

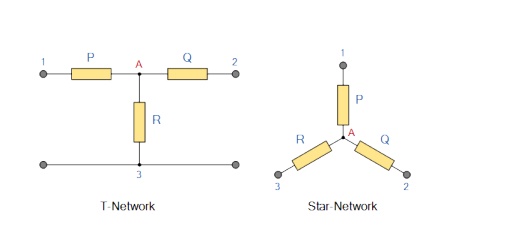
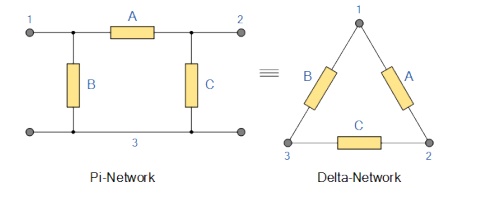
As we have already seen, we can redraw the T resistor network to produce an equivalent Star or Υ type network. But we can also convert a Pi or π type resistor network into an equivalent Delta or type network as shown below.

Pi-connected and Equivalent Delta Network.

_{Having  now  defined  exactly  what is  a Star and Delta connected network  it  is  possible  to transform the Υ into an equivalent circuit and also to convert a into an equivalent Υ circuit} using a the transformation process. This process allows us to produce a mathematical relationship between the various resistors giving us a Star Delta Transformation as well as a Delta Star Transformation.

These Circuit Transformations allow us to change the three connected resistances (or impedances) by their equivalents measured between the terminals 1-2, 1-3 or 2-3 for either a star or delta connected circuit. However, the resulting networks are only equivalent for voltages and currents external to the star or delta networks, as internally the voltages and currents are different but each network will consume the same amount of power and have the same power factor to each other.

The value of the resistor on any one side of the delta, network is the sum of all the two-product combinations of resistors in the star network divide by the star resistor located “directly opposite” the delta resistor being found.

For example, resistor A is given as:

A= (PQ + QR + RP) / R with respect to terminal 3 and resistor B is given as:

B = (PQ + QR + RP) / Q with respect to terminal 2 and resistor C given as:

B = (PQ + QR + RP) / R with respect to terminal 1.

By dividing out each equation by the value of the denominator we end up with three separate transformation formulas that can be used to convert any Delta resistive network into an equivalent star network as given below.

Star Delta Transformation allows us to convert one type of circuit connection into another type in order for us to easily analyze the circuit and star delta transformation techniques can be used for either resistances or impedances.

One final point about converting a star resistive network to an equivalent delta network. If all the resistors in the star network are all equal in value then the resultant resistors in the equivalent delta network will be three times the value of the star resistors and equal, giving: R_DELTA = 3R_STAR

Delta to Star Transformation

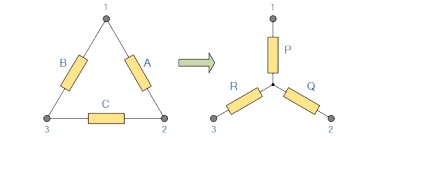
Compare the resistances between terminals 1 and 2.

P+Q= A in parallel with (B+C)

P+Q = A(B+C) / A+B+C……………….(1)

Resistance between the terminals 2 and 3.

Q+R = C in parallel with (A+B)

Q+R=C(A+B) / A+B+C……………….(2)

Resistance between the terminals 1 and 3.

P+R = B in parallel with (A+C)

P+R = B(A+C) / A+B+C………………(3)

This now gives us three equations and taking equation 3 from equation 2 gives: P+R-Q-R = (B(A+C)) –( C(A+B) ) / A+B+C

P-Q =(BA + BC – CA – BC) / A+B+C P-Q = BA – CA / (A+B+C)…………….(4)

Then, re-writing Equation 1 will give us:

P+Q = (AB+AC) / A+B+C …………………….(5)

Equ (4) + Equ (5)

P+Q+ P-Q = (AB+AC) / A+B+C + (BA – CA) / A+B+C 2P = (AB+AC+BA-CA) / A+B+C

2P = 2AB / A+B+C P = AB / A+B+C

Then to summarize a little about the above maths, we can now say that resistor P in a Star network can be found as Equation 1 plus (Equation 3 minus Equation 2) or Eq1 + (Eq3 – Eq2). Similarly, to find resistor Q in a star network, is equation 2 plus the result of equation 1 minus equation 3 or Eq2 + (Eq1 – Eq3) and this gives us the transformation of Q as:

Q = AC / A+B+C

and again, to find resistor R in a Star network, is equation 3 plus the result of equation 2 minus equation 1 or Eq3 + (Eq2 – Eq1) and this gives us the transformation of R as:

R = BC / A+B+C

When converting a delta network into a star network the denominators of all of the transformation formulas are the same: A + B + C, and which is the sum of ALL the delta resistances. Then to convert any delta connected network to an equivalent star network

If the three resistors in the delta network are all equal in value then the resultant resistors in the equivalent star network will be equal to one third the value of the delta resistors, giving each branch in the star network as: R_STAR = 1/3R_DELTA