Introduction to AC Circuits

AC Instantaneous and RMS:

Instantaneous Value:

The Instantaneous value of an alternating voltage or current is the value of voltage or current at one particular instant. The value may be zero if the particular instant is the time in the cycle at which the polarity of the voltage is changing. It may also be the same as the peak value, if the selected instant is the time in the cycle at which the voltage or current stops increasing and starts decreasing. There are actually an infinite number of instantaneous values between zero and the peak value.

RMS Value:

The average value of an AC waveform is NOT the same value as that for a DC waveforms average value. This is because the AC waveform is constantly changing with time and the heating effect given by the formula ( P = I ².R ), will also be changing producing a positive power consumption. The equivalent average value for an alternating current system that provides the same power to the load as a DC equivalent circuit is called the "effective value". This effective power in an alternating current system is therefore equal to: ( I².R. Average).

As power is proportional to current squared, the effective current, I will be equal to √ I 2 Ave. Therefore, the effective current in an AC system is called the Root Mean Squared or R.M.S.

Pure Resistive circuit:

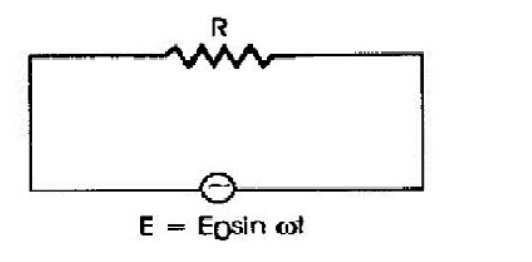
Resistors are “passive” devices that are they do not produce or consume any electrical energy, but convert electrical energy into heat. In DC circuits the linear ratio of voltage to current in a resistor is called its resistance. However, in AC circuits this ratio of voltage to current depends upon the frequency and phase difference or phase angle ( φ ) of the supply. So when using resistors in AC circuits the term Impedance, symbol Z is the generally used and we can say that DC resistance = AC impedance, R = Z.

It is important to note, that when used in AC circuits, a resistor will always have the same resistive value no matter what the supply frequency from DC to very high frequencies, unlike capacitor and inductors.

For resistors in AC circuits the direction of the current flowing through them has no effect on the behaviour of the resistor so will rise and fall as the voltage rises and falls. The current and voltage reach maximum, fall through zero and reach minimum at exactly the same time. i.e, they rise and fall simultaneously and are said to be “in-phase” as shown below.

We can see that at any point along the horizontal axis that the instantaneous voltage and current are in-phase because the current and the voltage reach their maximum values at the same time, that is their phase angle θ is 0^o. Then these instantaneous values of voltage and current can be compared to give the ohmic value of the resistance simply by using ohms law. Consider below the circuit consisting of an AC source and a resistor.

The instantaneous voltage across the resistor, V_R is equal to the supply voltage, V_t and is given as:

V_R = V_max sinωt

The instantaneous current flowing in the resistor will therefore be:

I_R = V_R / R

= V_max sinωt / R

= I _max sinωt

In purely resistive series AC circuits, all the voltage drops across the resistors can be added together to find the total circuit voltage as all the voltages are in-phase with each other. Likewise, in a purely resistive parallel AC circuit, all the individual branch currents can be added together to find the total circuit current because all the branch currents are in-phase with each other.

Since for resistors in AC circuits the phase angle φ between the voltage and the current is zero, then the power factor of the circuit is given as cos 0^o = 1.0. The power in the circuit at any instant in time can be found by multiplying the voltage and current at that instant.

Then the power (P), consumed by the circuit is given as P = Vrms Ι cos Φ in watt’s. But since cos Φ = 1 in a purely resistive circuit, the power consumed is simply given as, P = Vrms Ι the same as for Ohm’s Law.

This then gives us the “Power” waveform and which is shown below as a series of positive pulses because when the voltage and current are both in their positive half of the cycle the resultant power is positive. When the voltage and current are both negative, the product of the two negative values gives a positive power pulse.

Then the power dissipated in a purely resistive load fed from an AC rms supply is the same as that for a resistor connected to a DC supply and is given as:

P = V rms * I rms

= I 2 rms * R

= V 2 rms / R

Pure Inductive circuits:

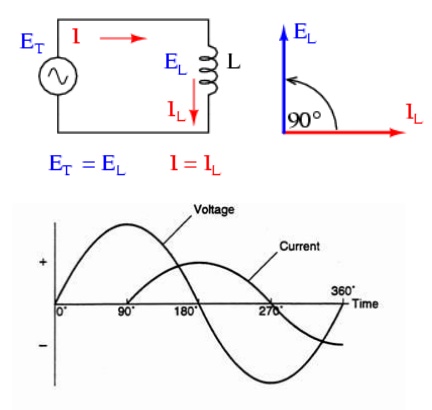
This simple circuit above consists of a pure inductance of L Henries ( H ), connected across a sinusoidal voltage given by the expression: V(t) = V_max sin ωt. When the switch is closed this sinusoidal voltage will cause a current to flow and rise from zero to its maximum value. This rise or change in the current will induce a magnetic field within the coil which in turn will oppose or restrict this change in the current.

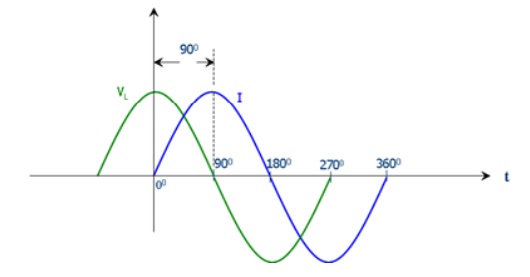
But before the current has had time to reach its maximum value as it would in a DC circuit, the voltage changes polarity causing the current to change direction. This change in the other direction once again being delayed by the self-induced back emf in the coil, and in a circuit containing a pure inductance only, the current is delayed by 90^o.

The applied voltage reaches its maximum positive value a quarter ( 1/4ƒ ) of a cycle earlier than the current reaches its maximum positive value, in other words, a voltage applied to a purely inductive circuit “LEADS” the current by a quarter of a cycle or 90^o as shown below.

The instantaneous voltage across the resistor, V_R is equal to the supply voltage, V_t and is given as:

V_L = V_max sin (ωt + 90)

I_L = V / X_L

X_L = 2πfL

Pure Capacitive circuits:

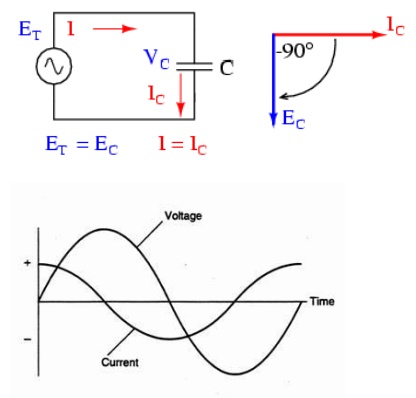
When the switch is closed in the circuit above, a high current will start to flow into the capacitor as there is no charge on the plates at t = 0. The sinusoidal supply voltage, V is increasing in a positive direction at its maximum rate as it crosses the zero reference axis at an instant in time given as 0^o. Since the rate of change of the potential difference across the plates is now at its maximum value, the flow of current into the capacitor will also be at its maximum rate as the maximum amount of electrons are moving from one plate to the other.

As the sinusoidal supply voltage reaches its 90^o point on the waveform it begins to slow down and for a very brief instant in time the potential difference across the plates is neither increasing nor decreasing therefore the current decreases to zero as there is no rate of voltage change. At this 90^opoint the potential difference across the capacitor is at its maximum ( V_max ), no current flows into the capacitor as the capacitor is now fully charged and its plates saturated with electrons.

At the end of this instant in time the supply voltage begins to decrease in a negative direction down towards the zero reference line at 180^o. Although the supply voltage is still positive in nature the capacitor starts to discharge some of its excess electrons on its plates in an effort to maintain a constant voltage. These results in the capacitor current flowing in the opposite or negative direction.

When the supply voltage waveform crosses the zero reference axis point at instant 180^o, the rate of change or slope of the sinusoidal supply voltage is at its maximum but in a negative direction, consequently the current flowing into the capacitor is also at its maximum rate at that instant. Also at this 180^o point the potential difference across the plates is zero as the amount of charge is equally distributed between the two plates.

Then during this first half cycle 0^o to 180^o, the applied voltage reaches its maximum positive value a quarter (1/4ƒ) of a cycle after the current reaches its maximum positive value, in other words, a voltage applied to a purely capacitive circuit “LAGS” the current by a quarter of a cycle or 90^o as shown below.

I_C = I_max sin (ωt + 90)

I_L = V / X_C

X_C = 1 / 2πfC

RL Series circuit:

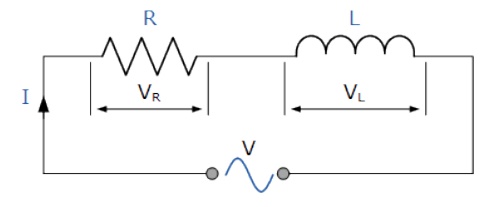
In othe r words, an Inductor in an electrical circuit opposes the flow of current, ( i ) through it. While this is perfectly correct, we made the assumption in the tutorial that it was an ideal inductor which had no resistance or capacitance associated with its coil windings.

However, in the real world “ALL” coils whether they are chokes, solenoids, relays or any wound component will always have a certain amount of resistance no matter how small associated with the coils turns of wire being used to make it as the copper wire will have a resistive value.

Then for real world purposes we can consider our simple coil as being an “Inductance”, L in series with a “Resistance”, R. In other words forming an LR Series Circuit.

A LR Series Circuit consists basically of an inductor of inductance L connected in series with a resistor of resistance R. The resistance R is the DC resistive value of the wire turns or loops that goes into making up the inductors coil

The above LR series circuit is connected across a constant voltage source, (the battery) and a switch. Assume that the switch, S is open until it is closed at a time t = 0, and then remains permanently closed producing a “step response” type voltage input. The current, i begins to flow through the circuit but does not rise rapidly to its maximum value of Imax as determined by the ratio of V / R(Ohms Law).

This limiting factor is due to the presence of the self induced emf within the inductor as a result of the growth of magnetic flux, (Lenz’s Law). After a time the voltage source neutralizes the effect of the self induced emf, the current flow becomes constant and the induced current and field are reduced to zero.

We can use Kirchoffs Voltage Law, ( Kirchoffs Voltage Law, (KVL) to define the individual voltage drops that exist around the circuit and then hopefully use it to give us an expression for the flow of current.

Vt = VR + VL

VR = I*R

VL = i dL / dt

V(t) =  I*R + i dL / dt

Since the voltage drop across the resistor, V_R is equal to IxR (Ohms Law), it will have the same exponential growth and shape as the current. However, the voltage drop across the inductor, V_L will have a value equal to: Ve^(-Rt/L). Then the voltage across the inductor, V_L will have an initial value equal to the battery voltage at time t = 0 or when the switch is first closed and then decays exponentially to zero as represented in the above curves.

The time required for the current flowing in the LR series circuit to reach its maximum steady state value is equivalent to about 5 time constants or 5τ. This time constant τ, is measured by τ = L/R, in seconds, were R is the value of the resistor in ohms and L is the value of the inductor in Henries. This then forms the basis of an RL charging circuit were 5τ can also be thought of as “5 x L/R” or the transient time of the circuit.

The transient time of any inductive circuit is determined by the relationship between the inductance and the resistance. For example, for a fixed value resistance the larger the inductance the slower will be the transient time and therefore a longer time constant for the LR series circuit. Likewise, for a fixed value inductance the smaller the resistance value the longer the transient time.

However, for a fixed value inductance, by increasing the resistance value the transient time and therefore the time constant of the circuit becomes shorter. This is because as the resistance increases the circuit becomes more and more resistive as the value of the inductance becomes negligible compared to the resistance. If the value of the resistance is increased sufficiently large compared to the inductance the transient time would effectively be reduced to almost zero.

RC Series circuit:

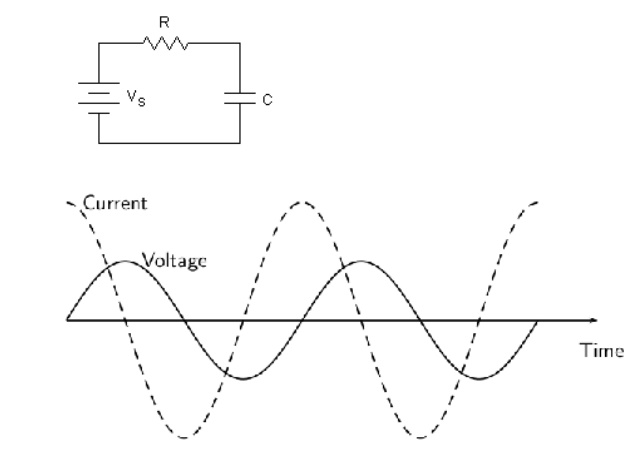
The fundamental passive linear circuit elements are the resistor (R), capacitor (C) and inductor (L). These circuit elements can be combined to form an electrical circuit in four distinct ways: the RC circuit, the RL circuit, the LC circuit and the RLC circuit with the abbreviations indicating which components are used. These circuits exhibit important types of behaviour that are fundamental to analogue electronics. In particular, they are able to act as passive filters. This article considers the RL circuit in both series and parallel as shown in the diagrams.

In practice, however, capacitors (and RC circuits) are usually preferred to inductors since they can be more easily manufactured and are generally physically smaller, particularly for higher values of components.

Both RC and RL circuits form a single-pole filter. Depending on whether the reactive element (C or L) is in series with the load, or parallel with the load will dictate whether the filter is low-pass or high-pass.

Frequently RL circuits are used for DC power supplies to RF amplifiers, where the inductor is used to pass DC bias current and block the RF getting back into the power supply.

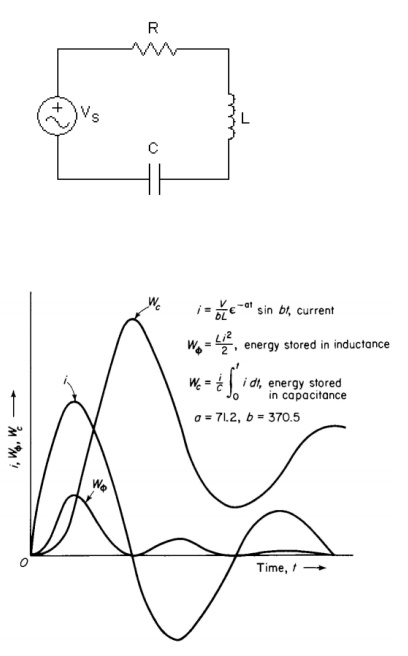
RLC Series Circuit:

Difference between AC AND DC:

Current that flows continuously in one direction is called direct current . Alternating current (A.C) is the current that flows in one direction for a brief time then reverses and flows in opposite direction for a similar time. The source for alternating current is called AC generator or alternator.

Cycle:

One complete set of positive and negative values of an alternating  quantity is called

cycle.

Frequency:

The number of cycles made by an alternating quantity per second is called frequency. The unit of frequency is Hertz(Hz)

Amplitude or Peak value

The maximum positive or negative value of an alternating quantity is called amplitude or peak value.

Average value:

This is the average of instantaneous values of an alternating quantity over one complete cycle of the wave.

Time period:

The time taken to complete one complete cycle.