Some binary operations on Boolean Matrices

Some binary operations on Boolean Matrices

Definition 12.3

A Boolean Matrix is a real matrix whose entries are either 0 or 1.

Note that the boolean entries 0 and 1 can be defined in several ways. In electrical switch to describe “on and off”, in graph theory, the “adjacency matrix” etc , the boolean entries 0 and 1 are used. We consider the same type of Boolean matrices in our discussion.

The following two kinds of operations on the collection of all boolean matrices are defined.

Let A = [a_ij] and B = [b_ij] be any two boolean matrices of the same type. Then their join ∨ and meet ∧ are defined as follows:

Definition 12.4: Join of A and B

A ∨ B =  [a_ij] ∨ [b_ij] = [a_ij ∨ b_ij] = [c_ij]

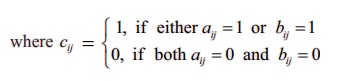
Definition 12.5: Meet of A and B

 A ∧ B = [a_ij] ∧ [b_ij] = [a_ij ∧ b_ij] = [c_ij]

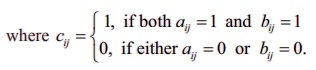
It is clear that ( a ∨ b) = max {a , b} ; ( a ∧ b) = min {a , b} , a , b ∈{0, 1}.

Example 12.8

Let 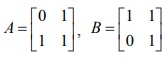 be any two boolean matrices of the same type. Find A ∨ B and A∧B.

Solution

Properties satisfied by join and meet

Let B be the set of all boolean matrices of the same type. We only state the properties of meet and join.

Closure property

A, B ∈ B, A ∨ B = [ a_ij ] ∨ [b_ij ] = [ a_ij ∨ b_ij ] ∈ B. (Because, ( a_ij ∨ b_ij ) is either 0 or 1 ∀i , j . ∨ is a binary operation on B.

Associative property

A∨(B∨C) = (A ∨ B) ∨ C, ∀A,B,C ∈ B. ∨ is associative.

Existence of identity property

∀A ∈ B, ∃ the null matrix 0 ∈  B ⋺ A ∨ 0 = 0 ∨ A = A . The identity element for ∨ is the null matrix.

Existence of inverse property

For any matrix A ∈ B, it is impossible to find a matrix

 B ∈ B  ⋺A ∨ B = B ∨ A = 0 . So the inverse does not exist.

Similarly, it can be verified that the operation meet ∧ satisfies (i) closure property (ii) commutative property (iii) associative property (iv) the matrix 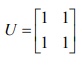 exists as the identity in B and (v) the existence of inverse is not assured.