Binary operations: Modular Arithmetic

Modular Arithmetic

Having discussed the properties of operations like basic usual arithmetic operations, matrix addition and multiplication, join and meet of boolean matrices, one more new operation called the Modular Arithmetic is discussed in this section. The modular arithmetic refers to the process of dividing some number a by a positive integer n ( > 1), called modulus, and then equating a with the remainder b modulo n and it is written as a ≡ b(mod n) , read as ‘a is congruent to b modulo n _’

Here a ≡ b (mod n ) means a − b = n ⋅ k for some integer k and b is the least non-negative integer when a is divided by n.

For instance, 25 ≡ 4(mod 7), −20 ≡ −2(mod 3) ≡ 1(mod 3) and 15 ≡ 0(mod 5), etc. Further the set of integers when divided by n , leaves the remainder 0, 1, 2, , n-1. In the case of  ℤ₅,

[0] = { .. ., −15, −10, −5, 0, 5,10,15, … }

[1] = {… , −14, −9, −4,1, 6, 11, …}

[2] = {… , −13, −8, −3, 2, 7,12,…]

[3] = {…, −12, −7, −2, 3,8,13,…}

[4] = {… , −11, −6, −1, 4, 9,14,…}.

We write this as ℤ₅ = {[0],[1],[ 2],[3],[ 4]} . In each class, any two numbers are congruent modulo 5.

Before 2007, modular arithmetic is used in 10-digit ISBN (International Standard Book Number) numbering system. For instance, the last digit is for parity check. It is from the set {0,1, 2,3, 4,5, 6, 7,8,9, X } . In ISBN number, 81-7808-755-3, the last digit 3 is obtained as

1*8+2*1+3*7+4*8+5*0+6*8+7*7+8*5+9*5=8+2+21+32+0+48+49+40+45=245 ≡ 3(mod11).

Alternatively, the weighted sum is calculated in the reverse manner

9*8+8*1+7*7+6*8+5*0+4*8+3*7+2*5+1*5=245 = 3 (mod 11).

In both ways, we get the same check number 3.

After 2007, 13-digit ISBN numbering has been followed. The first 12 digits (from left to right) are multiplied by the weights 3,1,3,1,…. starting from right to left. Then the weighted sum is calculated.

The higher multiple of 10 is taken. Then the difference is calculated. Then its additive inverse modulo 10 is the thirteenth digit.

For instance, consider the ISBN Number: 978-81-931995-6-5.Take 12 digits from left to right.

The total of last row is 155. The nearest (higher) integer in multiples of 10 is 160. The difference 160-155=5. The additive inverse modulo 10 is 5 which is 13-th digit in the ISBN number.

Two new operations namely addition modulo n( +_n ) and multiplication modulo n(×_n ) are defined on the set ℤ_n of all non-negative integers less than n under modulo arithmetic.

Definition 12.6

(i) The addition modulo n is defined as follows.

Let a,b ∈ ℤ_n . Then

a + _nb = the remainder of a + b on division by n .

(ii) The multiplication modulo n is defined as follows.

Let a,b ∈ ℤ_n . Then

a × _n b the remainder of a ×b on division by n

Example 12.9

Verify (i) closure property, (ii) commutative property, (iii) associative property, (iv) existence of identity, and (v) existence of inverse for the operation +₅ on ℤ₅ using table corresponding to addition modulo 5.

Solution

It is known that ℤ₅ = {[ 0 ], [1], [2], [3], [4]} . The table corresponding to addition modulo 5 is as follows: We take reminders {0,1, 2, 3, 4} to represent the classes {[0],[1],[2],[3],[4]} .

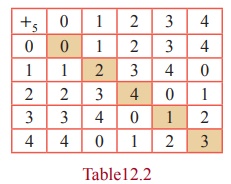
(i) Since each box in the table is filled by exactly one element of ℤ₅ , the output a +₅ b is unique and hence +₅ is a binary operation.

(ii) The entries are symmetrically placed with respect to the main diagonal. So +₅ has commutative property.

(iii) The table cannot be used directly for the verification of the associative property. So it is to be verified as usual.

For instance, ( 2 + ₅ 3) +₅ 4 = 0 +₅ 4 = 4 (mod 5)

and 2 + ₅ ( 3 +₅ 4 ) = 2 +₅ 2 = 4( mod 5) .

Hence ( 2 +₅ 3) + ₅ 4 = 2 + ₅ ( 3 +₅ 4) .

Proceeding like this one can verify this for all possible triples and ultimately it can be shown that +₅ is associative.

(iv) The row headed by 0 and the column headed by 0 are identical. Hence the identity element is 0.

(v) The existence of inverse is guaranteed provided the identity 0 exists in each row and each column. From Table12.2, it is clear that this property is true in this case. The method of finding the inverse of any one of the elements of ℤ₅ , say 2 is outlined below.

First find the position of the identity element 0 in the III row headed by 2. Move horizontally along the III row and after reaching 0, move vertically above 0 in the IV column, because 0 is in the III row and IV column. The element reached at the topmost position of IV column is 3. This element 3 is nothing but the inverse of 2, because, 2 + ₅ 3 = 0 (mod 5) . In this way, the inverse of each and every element of ℤ₅ can be obtained. Note that the inverse of 0 is 0,that of 1 is 4, that of 2 is 3, that of 3 is 2 , and, that of 4 is 1.

Example 12.10

Verify (i) closure property, (ii) commutative property, (iii) associative property, (iv) existence of identity, and (v) existence of inverse for the operation ×₁₁ on a subset A = {1, 3, 4, 5, 9} of the set of remainders {0,1, 2,3, 4,5, 6, 7,8,9,10}.

Solution

The table for the operation ×₁₁ is as follows.

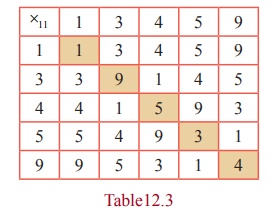
Following the same kind of procedure as explained in the previous example, a brief outline of the process of verification of the properties of ×₁₁ on A is given below.

(i) Since each box has an unique element of A, ×₁₁ is a binary operation on A.

(ii) The entries are symmetrical about the main diagonal. Hence ×₁₁ has commutative property.

(iii) As usual, the associative property can be seen to be true.

(iv) The entries of both the row and column headed by the element 1 are identical. Hence 1 is the identity element.

(v) Since the identity 1 exists in each row and each column, the existence of inverse property is assured for ×₁₁ . The inverse of 1 is 1, that of 3 is 4, that of 4 is 3, 5 is 9 , and, that of 9 is 5.