Exercise 12.2: Mathematical Logic

EXERCISE 12.2

1. Let p : Jupiter is a planet and q : India is an island be any two simple statements. Give  verbal sentence describing each of the following statements.

 (i) ¬p (ii) p ∨ ¬q  (iii) ¬p ∨ q (iv) p → ¬q (v) p ↔ q

2. Write each of the following sentences in symbolic form using statement variables p and q .

(i) 19 is not a prime number and all the angles of a triangle are equal.

(ii) 19 is a prime number or all the angles of a triangle are not equal

(iii) 19 is a prime number and all the angles of a triangle are equal

(iv) 19 is not a prime number

3. Determine the truth value of each of the following statements

(i) If 6 + 2 = 5 , then the milk is white.

(ii) China is in Europe or √3 is an integer

(iii) It is not true that 5 + 5 = 9 or Earth is a planet

(iv) 11 is a prime number and all the sides of a rectangle are equal

4. Which one of the following sentences is a proposition?

(i) 4 + 7 = 12 (ii) What are you doing? (iii) 3n ≤ 81, n ∈ ℕ (iv) Peacock is our national bird (v) How tall this mountain is!

5. Write the converse, inverse, and contrapositive of each of the following implication.

(i) If x and y are numbers such that x = y , then x2 = y2

(ii) If a quadrilateral is a square then it is a rectangle

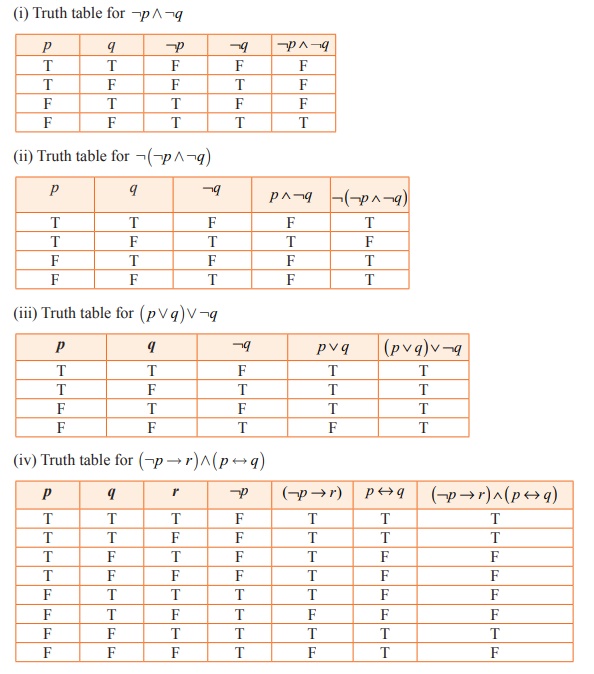
6. Construct the truth table for the following statements.

(i) ¬ p ∧ ¬q (ii) ¬( p ∧ ¬q) (iii) ( p ∨ q ) ¬q (iv) (¬ p → r) ∧ ( p ↔ q)

7. Verify whether the following compound propositions are tautologies or contradictions or Contingency

(i) ( p ∧ q ) ¬( p ∨ q)

(ii) ( ( p ∨ q) ¬p ) → q

(iii) ( p → q ) ↔ (¬ p → q)

(iv) ( ( p → q ) ∧ (q → r))→ ( p → r)

8. Show that (i) ¬( p ∧ q) ≡ ¬p ∨¬q  (ii) ¬( p → q) ≡ p ∧¬q .

9. Prove that q → p ≡¬ p →¬q

10. Show that p → q and q → p are not equivalent

11. Show that ¬( p ↔ q) ≡ p ↔¬q

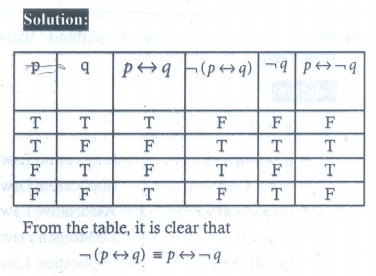
12. Check whether the statement p → ( q → p) is a tautology or a contradiction without using the truth table.

13. Using truth table check whether the statements¬( p ∨ q ) ∨ (¬p ∧ q) and ¬p are logically equivalent.

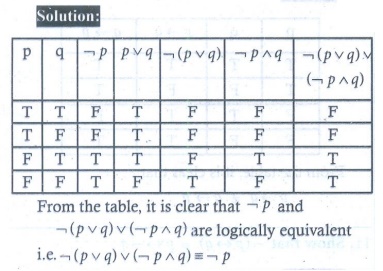
14. Prove p → ( q → r) ≡ ( p ∧ q) → r without using truth table.

15. Prove that p → (¬q ∨ r ) ≡ ¬p ∨ (¬q ∨ r) using truth table.

Answers:

1. (i) ¬p : Jupiter is not a planet (ii) p ∧ ¬q : Jupiter is a planet and India is not an Island.

(iii) ¬ p ∨ q : Jupiter is not a planet or India is an Island.

(iv) p → ¬q : If Jupiter is a planet then India is not an Island.

(v) p ↔ q Jupiter is a planet if and only if India is an Island.

2. (i) ¬ p ∧ q     (ii) p ∨ ¬q   (iii) p ∧ q  (iv) ¬p

3. (i) p → q is T (ii) p ∨ q  is F (iii) ¬ p ∨ q is T (iv) p ∧ q  is F

4. (i), (iii) and (iv) are propositions

5. (i) Converse: If x and y are numbers such that x2 = y2 then x = y .

Inverse: If x and y are numbers such that x ≠ y then x2 ≠ y2.

Contra positive: If x and y are numbers such that x2 ≠ y2 then x ≠ y .

(ii) Converse: If a quadrilateral is a rectangle then it is a square.

Inverse: If a quadrilateral is not a square then it is not a rectangle.

Contrapositive: If a quadrilateral is not a rectangle then it is not a square.

6. 

7. (i) Contradiction  (ii) Tautology  (iii) Contingency  (iv) Tautology

12. p → ( q → p) is a Tautology.

13. Yes. The statements are logically equivalent.