Exercise 12.1: Binary operations

EXERCISE 12.1

1. Determine whether ∗ is a binary operation on the sets given below.

(i) a ∗ b = a. |b| on ℝ (ii) a ∗ b = min ( a , b) on A = {1, 2, 3, 4, 5}

(iii) ( a ∗ b) = a√b is binary on ℝ.

2. On ℤ, define ∗ by ( m ∗ n)= mn + nm : ∀ m, n ∈ ℤ. Is ∗ binary on ℤ?

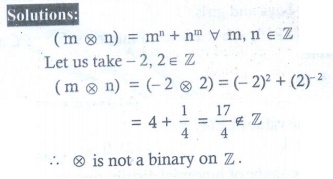
3. Let ∗ be defined on ℝ by ( a ∗ b) = a + b + ab − 7 . Is ∗ binary on ℝ ? If so, find 3∗ (-7/15).

4. Let A = {a + √5b : a, b ∈ ℤ } . Check whether the usual multiplication is a binary operation on A .

5. (i) Define an operation ∗ on ℚ as follows: a ∗ b = ( a+b / 2); a , b ∈ ℚ. Examine the closure, commutative, and associative properties satisfied by ∗ on ℚ.

(ii) Define an operation ∗ on ℚ as follows: a ∗ b = = ( a+b / 2); a , b ∈ ℚ. Examine the existence of identity and the existence of inverse for the operation ∗ on ℚ.

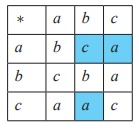
6. Fill in the following table so that the binary operation ∗ on A = {a , b , c} is commutative.

7. Consider the binary operation ∗ defined on the set A = {a , b, c, d} by the following table:

Is it commutative and associative?

8. Let 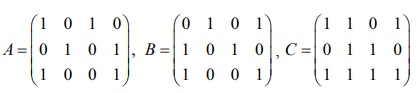 be any three boolean matrices of the same type. Find (i) A ∨ B (ii) A ∧ B (iii) ( A ∨ B)∧ C (iv) ( A ∧ B)∨ C .

9. (i) Let 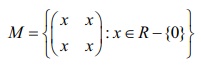 and let ∗ be the matrix multiplication. Determine whether M is closed under ∗ . If so, examine the commutative and associative properties satisfied by ∗ on M .

(ii) Let 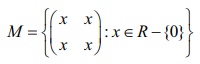 and let ∗ be the matrix multiplication. Determine whether M is closed under ∗ . If so, examine the existence of identity, existence of inverse properties for the operation ∗ on M.

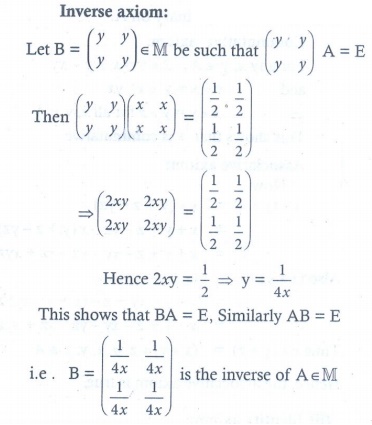
10. (i) Let A be ℚ\{1}. Define ∗ on A by x ∗ y = x + y − xy . Is ∗ binary on A ? If so, examine the commutative and associative properties satisfied by ∗ on A .

(ii) Let A be ℚ \{1}. Define ∗ on A by x ∗ y = x + y − xy . Is ∗ binary on A ? If so, examine the existence of identity, existence of inverse properties for the operation ∗ on A .

Answers:

(i) Yes, * is binary on ℝ (ii) Yes, * is binary on A (iii) No, * is not binary on ℝ

2. No, * is not binary on ℤ

3. -88/15

4. Yes, usual multiplication is binary on A

5. (i) The given operation * is closure and commutative but not associative on ℚ.

(ii) Identity does not exist and so inverse does not exist.

6. 

7. No. The given operation is not commutative and associative

8. 

10. (i) It is commutative and associative. (ii) Identity and Inverse is exist.