Mathematical Logic: Tautology, Contradiction, and Contingency

Mathematical Logic

Tautology, Contradiction, and Contingency

Definition 12.16

A statement is said to be a tautology if its truth value is always T irrespective of the truth values of its component statements. It is denoted by T.

Definition 12.17

A statement is said to be a contradiction if its truth value is always F irrespective of the truth values of its component statements. It is denoted by F.

Definition 12.18

A statement which is neither a tautology nor a contradiction is called contingency

Observations

1. For a tautology, all the entries in the column corresponding to the statement formula will contain T.

2. For a contradiction, all the entries in the column corresponding to the statement formula will contain F.

3. The negation of a tautology is a contradiction and the negation of a contradiction is a tautology.

4. The disjunction of a statement with its negation is a tautology and the conjunction of a statement with its negation is a contradiction. That is p ∨¬p is a tautology and p ∧¬p is a contradiction. This can be easily seen by constructing their truth tables as given below.

Example for tautology

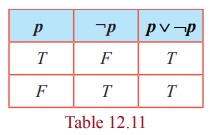
Since the last column of p ∨ ¬p contains only T, p ∨ ¬p is a tautology.

Example for contradiction

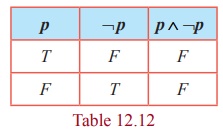
Since the last column contains only F, p ∧ ¬p is a contradiction.

Note

All the entries in the last column of Table 12.10 are F and hence ( p ⊽ q) ∧ ( p ⊽ ¬q) is a contradiction.

Example for contingency

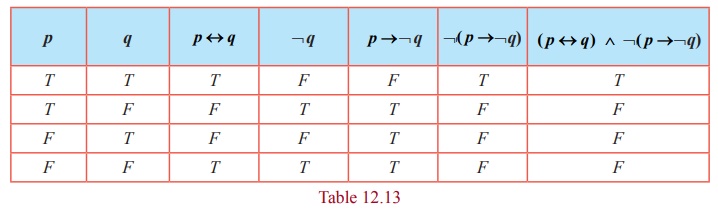
In the above truth table, the entries in the last column are a combination of T and F. The given statement is neither a tautology nor a contradiction. It is a contingency.