Definitions of Binary Operations

Binary Operations

Definitions

The basic arithmetic operations ℝ on are addition (+), subtraction (−), multiplication (×), and division (÷). Eminent mathematicians of the latter part of 19^th century and in 20^th century like Abel, Cayley, Cauchy, and others, tried to generalize the properties satisfied by these usual arithmetic operations. To this end they developed new abstract algebraic structures through the axiomatic approach. This new branch of algebra dealing with these abstract algebraic structures is known as abstract algebra.

To begin with, consider a simple example involving the basic usual arithmetic operations addition and multiplication of any two natural numbers.

  m + n ∈ ℕ ; m × n ∈ ℕ, ∀m, n ∈ ℕ = {1, 2, 3,...}

Each of the above two operations yields the following observations:

(1) At a time exactly two elements of ℕ are processed.

(2) The resulting element (outcome) is also an element of ℕ.

Any such operation defined on a nonempty set is called a binary operation or a binary composition on the set in abstract algebra.

Definition 12.1

Any operation _* defined on a non-empty set S is called a binary operation on S if the following conditions are satisfied:

(i) The operation _* must be defined for each and every ordered pair (a , b) ∈ S × S .

(ii) It assigns a unique element a∗b of S to every ordered pair (a , b) ∈ S × S .

In other words, any binary operation _* on S is a rule that assigns to each ordered pair of elements of S a unique element of S . Also _* can be regarded as a function (mapping) with input in the Cartesian product S × S and the output in S .

 ∗ : S × S → S ; ∗( a , b) = a ∗ b ∈ S , where a *b is an unique element.

A binary operation defined by ∗ : S × S → S ; ∗( a , b) = a ∗ b ∈ S demands that the output a ∗b must always lie the given set S and not in the complement of it. Then we say that ‘ ∗ is closed on S ’ or ‘ S is closed with respect to ∗ ’. This property is known as the closure property.

Definition 12.2

Any non-empty set on which one or more binary operations are defined is called an algebraic structure.

Another way of defining a binary operation ∗ on S is as follows:

 ∀ a , b ∈ S , a∗b is unique and a ∗ b ∈ S .

Note

It follows that every binary operation satisfies the closure property.

Note

The operation ∗ is just a symbol which may be + , ×, −, ÷ matrix addition, matrix multiplication, etc. depending on the set on which it is defined.

For instance, though + and × are binary on ℕ, −  is not binary operation on ℕ.

To verify this, consider (3, 4) ∈ ℕ × ℕ.

 ∗ ( a , b) = − (3, 4) = 3 − 4 = −1 ∉ ℕ.

Hence −  is not binary operation on ℕ. So ℕ is to be extended to ℤ in order that − becomes binary operation on ℤ. Thus ℤ is closed with respect to + , ×, and − . Thus (ℤ, + , ×, −) is an algebraic structure.

Observations

The binary operation depends on the set on which it is defined.

(a) The operation – which is not binary operation on ℕ but it is binary on ℤ. The set ℕ is extended to include negative numbers. We call the included set ℤ.

(b) The operation ÷ on ℤ is not binary operation on ℤ. For instance, for (1, 2) ∈ ℤ × ℤ, ÷ (1, 2) = 1/2 ∉ ℤ. Hence ℤ has to be extended further into ℚ.

(c) It is a known fact that the division by 0 is not defined in basic arithmetic. So ÷ is binary operation on the set ℚ\{0}. Thus + , ×, − are binary operation on ℚ and ÷ is binary operation ℚ on \{0}.

Now the question is regarding the reasons for extending further ℚ to and then from ℚ  to C. Accordingly, a number system is needed where not only all the basic arithmetic operations +, −, ×, ÷ but also to include the roots of the equations of the form “ x² − 2 = 0 ” and“ x² + 1 = 0 ”.

So, in addition to the existing systems, the collection of irrational numbers and imaginary numbers (See Chapter 3) are to be adjoined. Consequently ℝ and then C are obtained. The biggest number system C properly includes all the other number systems ℕ, ℤ, ℚ, and ℝ as subsets.

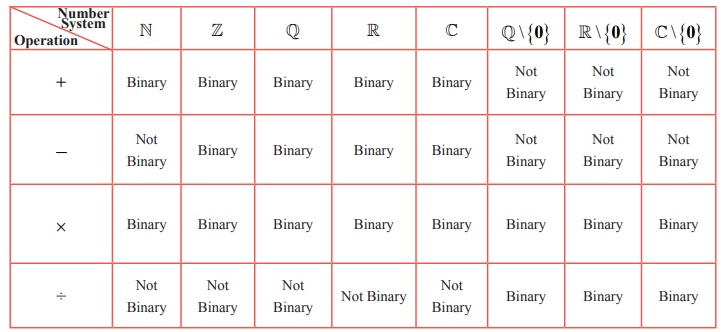
Table12.1

Example12.1

Examine the binary operation (closure property) of the following operations on the respective sets (if it is not, make it binary):

(i) a ∗ b = a + 3ab − 5b²  ; ∀ a,b ∈ ℤ

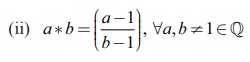
Solution

(i) Since × is binary operation on ℤ, a , b ∈ ℤ ⇒ a × b = ab ∈ ℤ and b × b = b² ∈ ℤ ... (1)

The fact that + is binary operation on ℤ and (1) ⇒ 3ab = ( ab + ab + ab) ∈ ℤ and

5b² = (b² + b² + b² + b² + b²) ∈ ℤ. .... (2)

Also a ∈ ℤ and 3ab ∈ ℤ implies a + 3ab ∈ ℤ. ... (3)

(2), (3), the closure property of − on ℤ yield a ∗ b = ( a + 3ab − 5b² ) ∈ ℤ. Since a ∗ b belongs to ℤ, * is a binary operation on ℤ.

(ii) In this problem a ∗b is in the quotient form. Since the division by 0 is undefined, the denominator b -1must be nonzero.

It is clear that b − 1 = 0 if b = 1. As 1∈ ℚ, ∗ is not a binary operation on the whole of ℚ.

However it can be found that by omitting 1 from ℚ, the output a ∗b exists in ℚ\{1} .

Hence ∗ is a binary operation on \{1} .