Mathematical Logic: Logical Connectives and their Truth Tables

Logical Connectives and their Truth Tables

(1) Truth Table for NOT [¬] (Negation)

Truth Table for ¬ p

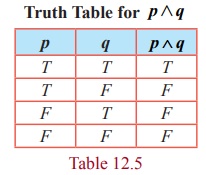
(2) Truth table for AND [ ∧ ] (Conjunction)

Truth Table for p Λ q

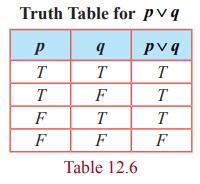
(3) The truth tables for OR [ ∨ ] (Disjunction)

Truth Table for p ∨ q

Example 12.12

Write the statements in words corresponding to ¬ p, p ∧ q , p ∨ q and q ∨ ¬p, where p is ‘It is cold’ and q is ‘It is raining.’

Solution

(i) ¬p : It is not cold.

(ii) p ∧ q : It is cold and raining.

(iii) p ∨ q : It is cold or raining.

(iv) q ∨ ¬p : It is raining or it is not cold

Observe that the statement formula ¬p has only 1 variable p and its truth table has 2 = ( 2¹ ) rows. Each of the statement formulae p ∧ q and p ∨ q has two variables p and q . The truth table corresponding to each of them has 4 = ( 2² ) rows. In general, it follows that if a statement formula involves n variables, then its truth table will contain 2ⁿ rows.

Example 12.13

How many rows are needed for following statement formulae?

(i) p ∨ ¬t ∧ ( p ∨ ¬s ) (ii) ( ( p ∧ q ) ∨ ( ¬r ∨ ¬s )) ∧ ( ¬t ∧ v)

Solution

(i) ( p ∨ ¬t ) ∧ ( p ∨ ¬s ) contains 3 variables p, s ,and t . Hence the corresponding truth table will contain 2³ = 8 rows.

(ii) ( ( p ∧ q) ∨ ( ¬ r ∨ ¬ s )) ∧ ( ¬ t ∧ v) contains 6 variables p, q, r, s,t , and v . Hence the corresponding truth table will contain 2⁶ = 64 rows.

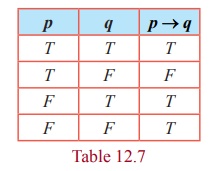
Conditional Statement

Definition 12.13

The conditional statement of any two statements p and q is the statement, “If p , then q ” and it is denoted by p → q . Here p is called the hypothesis or antecedent and q is called the conclusion or consequence. p → q is false only if p is true and q is false. Otherwise it is true.

Truth table for p → q

Example 12.14

Consider p → q : If today is Monday, then 4 + 4 = 8.

Here the component statements p and q are given by,

p: Today is Monday; q: 4 + 4 = 8.

The truth value of p → q is T because the conclusion q is T.

An important point is that p → q should not be treated by actually considering the meanings of p and q in English. Also it is not necessary that p should be related to q at all.

Consequences

From the conditional statement p → q _, three more conditional statements are derived. They are listed below.

(i) Converse statement q → p _.

(ii) Inverse statement ¬ p →¬q .

(iii) Contrapositive statement ¬ q →¬p .

Example 12.15

Write down the (i) conditional statement (ii) converse statement (iii) inverse statement, and (iv) contrapositive statement for the two statements p and q given below.

 p : The number of primes is infinite. q: Ooty is in Kerala.

Solution

Then the four types of conditional statements corresponding to p and q are respectively listed below.

(i) p → q : (conditional statement) “If the number of primes is infinite then Ooty is in Kerala”.

(ii) q → p : (converse statement) “If Ooty is in Kerala then the number of primes is infinite”

(iii) ¬ p →¬q (inverse statement) “If the number of primes is not infinite then Ooty is not in Kerala”.

(iv) ¬ q →¬p (contrapositive statement) “If Ooty is not in Kerala then the number of primes is not infinite”.

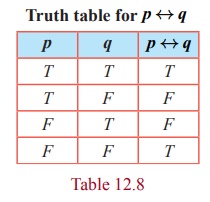
Bi-conditional Statement

Definition 12.14

The bi-conditional statement of any two statements p and q is the statement “ p if and only if q ” and is denoted by p ↔ q . Its truth value is T , whenever both p and q have the same truth values, otherwise it is false.

Truth table for p ↔ q

Exclusive OR (EOR)[ ⊽ ]

Definition 12.15

Let p and q be any two statements. Then p EOR q is such a compound statement that its truth value is decided by either p or q but not both. It is denoted by p ⊽ q . The truth value of p ⊽ q is T whenever either p or q is T, otherwise it is F. The truth table of p ⊽ q is given below.

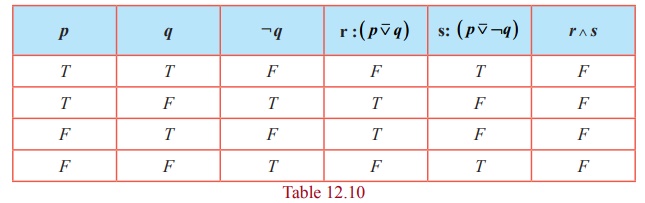
Example 12.16

Construct the truth table for ( p ⊽ q) ∧ ( p ⊽ ¬q) .

Also the above result can be proved without using truth tables. This proof will be provided after studying the logical equivalence.