Separation between Lattice Planes in a cubic Crystal

Separation between Lattice Planes in a cubic Crystal

Consider a cubic crystal with cube edge a. let (h,k,l) be the Miller Indices of the plane ABC.

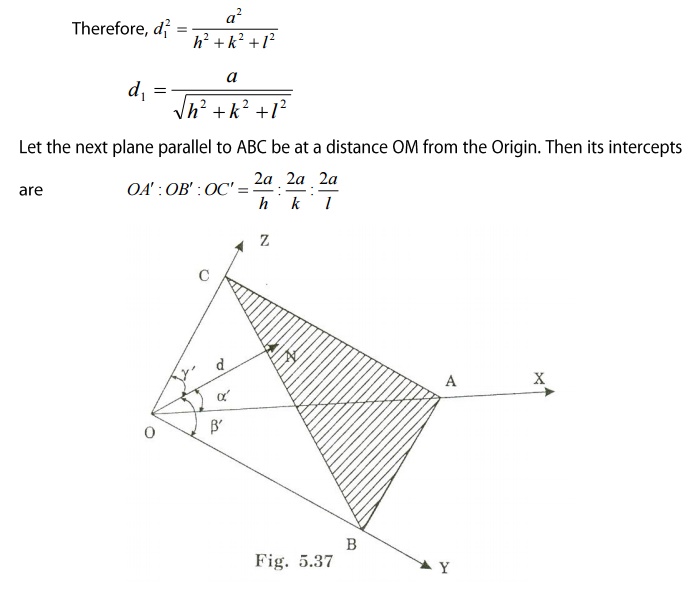
Fig 1.1.6 Separation between Lattice Planes in a cubic Crystal

Let ON=d be a normal to the plane passing through the origin O. On makes angles  α’,β’,γ’ with x,y and z-axis respectively. The direction cosines, cos α’, cosβ’ and cosγ’ are written as

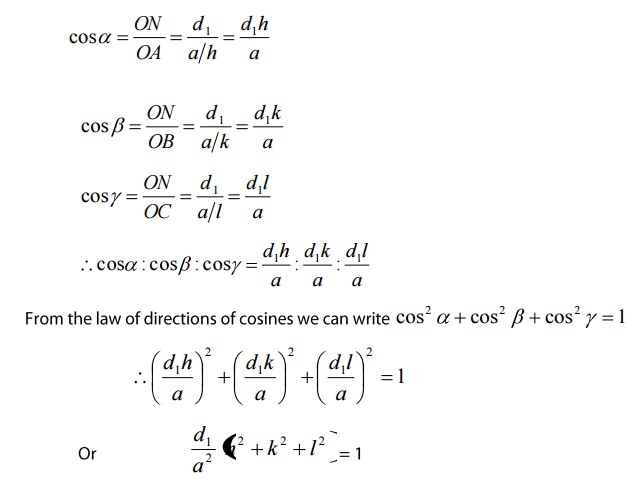
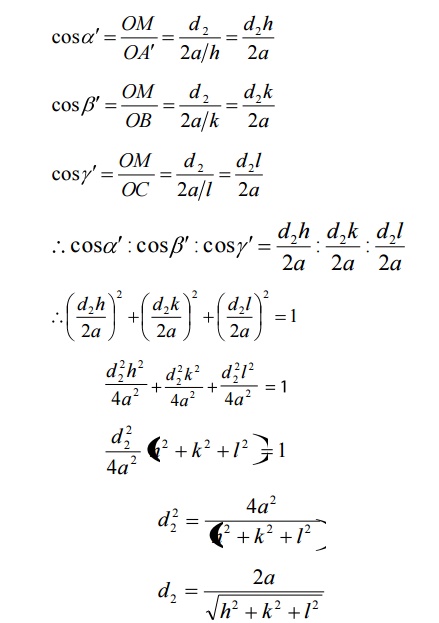
Interplanar distance d:

We know interplanar distance is the distance between two successive planes. Since ‘d’ is the distance between the two planes ABC and A’B’C’, we can write the interplanar distance ‘d’ as

D=d₂-d₁

Interplanar distance

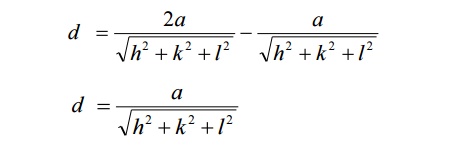
Fundamental Crystallographic terms

Lattice is defined as an array of points which are imaginarily kept to represent the position of atoms in the crystal that every lattice point has got the same environment as that o the other and hence one lattice point cannot be distinguished from the other lattice point.

Space Lattice or Crystal Lattice is a three dimensional collection of points in space. The environment about any particular point is in everyway the same.

The regular pattern of points which describe the three dimensional arrangement of particles in a crystal structure is called the Crystal Lattice or Space lattice.

Basis is formed by associating with every lattice point a uint of assembly of atoms or molecules identical in composition. This unit assembly is called Basis.

The Crystal Structure is formed by the addition of a basis to every lattice point.