Body centered cubic(BCC) Structure

Body centered cubic (BCC) Structure

In body centered cubic structure, the unit cell has one atom at each corner of the cube and one at body center of the cube. Figure 3.8 shows the arrangement of the atoms in a bcc cell.

(i)                Number of atoms per unit cell

In a body centered crystal structure, the atoms touch along the diagonal of the body. Each and every corner atoms are shared by eight adjacent unit cells. Therefore, the total number of atoms contributed by the corner atoms is 1/8 x 8 =1 atom.

One full atom at the center of the unit cell = 1 atom

Therefore, total number of atoms present in the bcc unit cell = 1+1 = 2 atoms.

(ii)             Coordination Number

The coordination number of the body centered cubic unit cell is calculated as follows.

Let us consider a body-centered atom. The nearest neighbor for a bcc atom is corner atom. A body centered atom is surrounded by 8 corner atoms. Therefore, the coordination number of a bcc unit cell is 8.

Atomic radius

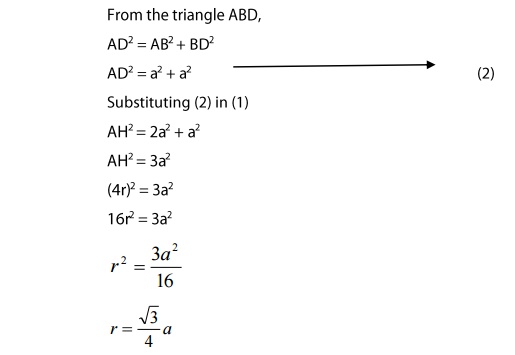
For a body centered unit cell, the atomic radius can be calculated as follows from figure as follows. From figure, AH = 4r and DH = a

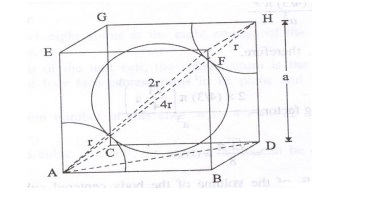
From the triangle AHD,

AH²=AD²+DH²  ----> (1)

(iii)           Packing Factor

The number of atoms present in a unit cell = 2 atoms

Packing Factor = (Number of atoms present per unit cell x Volume of atom) / Volume of the Unit Cell

Number of atoms per unit cell=2

Therefore, we can say that 68% volume of the unit cell of BCC is occupied by atoms and remaining 32% volume is vacant.

Thus the Packing Density is 68%.

Since the packing density is greater than simple than cubic, it has tightly packed structure, when compared to SC.