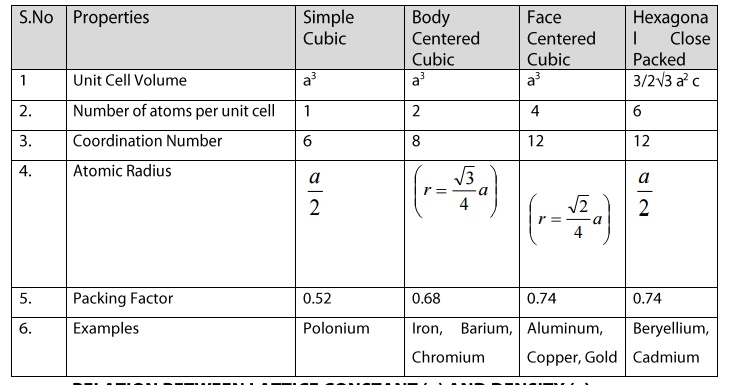
Properties of some Crystal Structure - Sodium choride, Diamond cubic

Properties of some Crystal Strucure

RELATION BETWEEN LATTICE CONSTANT (a) AND DENSITY(ρ)

Consider a cubic crystal of lattice constant a

Density of the crystal = ρ

Volume of the unit cell = a³

Mass of the unit cell = ρ a³

Density = mass /volume

Number of atoms per unit = n

Atomic weight of the material = M

Avogadro’s number =N

Avogadro’s number is the number of atoms per kg mole of the substance.

Mass of each atom = M/N

Mass of the unit cell = mass of the each atom in unit cell x number of atoms per unit cell

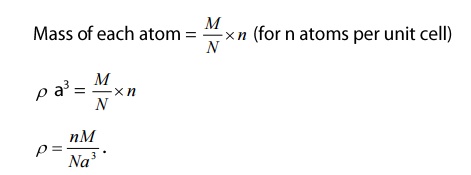
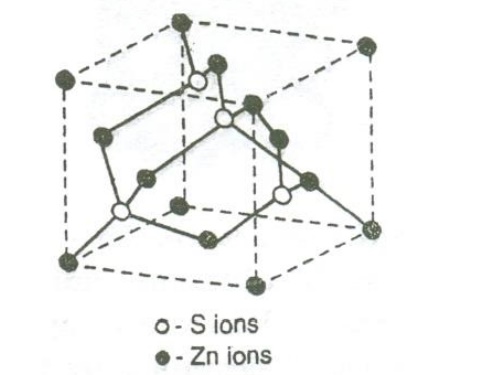
Diamond cubic structure:

Diamond has face centered structure (FCC) with the basis of two carbon atoms viz., ‘X’ and ‘Y’. The ‘X’ atom is located with an origin (0, 0, 0) and the Y atom is located with an orgin of (a/4 , a/4, a/4) (i.e) one quarter of the way along the body diagonal as shown in the figure

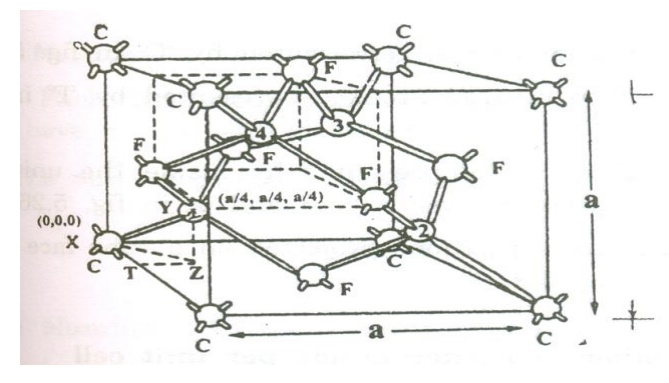
Thus from the figure we can see that diamond structure is formed due to the combination of two interpenetrating FCC sub lattices, having the origin (0,0,0) and (1/4,1/4,1/4) along the body diagonal.

Let us now discuss some of the important parameters of the diamond

1.     Number of atoms per unit cell

i.                   Corner atoms, represented by ‘F’ as shown in the figure

ii.                 Face centered atoms, represented by ‘F’ as shown in the figure.

iii.              Four atoms present inside the unit cell an s represented as 1, 2.3,4 as shown in the figure.

iv.              The three type of atoms positions projected on a cube face is as shown.

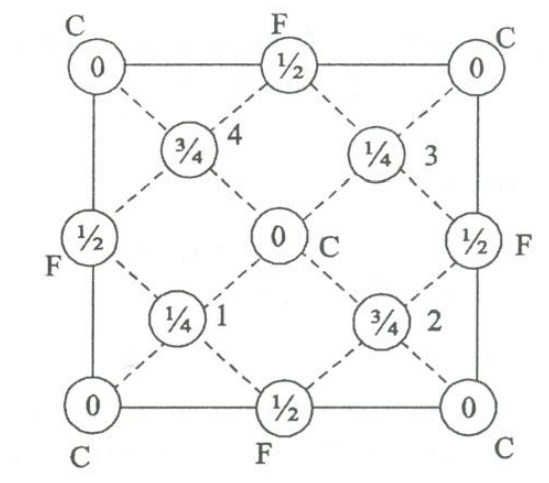
i.                   Number of atoms per unit cell:

Each corner atom is shared by 8 unit cells. Similarly we have 8 corner atoms in an unit cell.

The number of corner atoms in an unit cell.

ii.                 Number of face centered atoms per unit cell

Each face centered atom is shared by 2 unit cells. Similarly, we   have 6 face centered atoms.

The number of face centered atom per unit cell  = ½ x 6 = 3 atoms

iii.  Number of atoms inside the unit cell

Inside the unit cell we have 4 atoms, represented by 1,2,3,4 in the figure which is shared by that particular unit cell alone.

 Total number of atoms per unit cell = 1+3+4=8

2.  Atomic radius

    We know atomic radius is defined as half the distance between any two nearest neighbor atoms, which have direct contact with each other.

   Here, the corner atoms do not have contact with each other and the face centered atoms also do not have contact with the corner atoms.  But both the face centered atoms and the corner atoms have contact with the 4 atoms           (1,2,3,4)

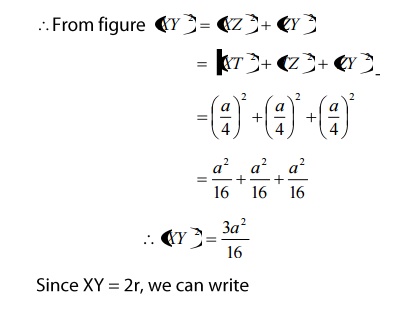
     From figure, we can see that the nearest two neighbors which have direct contact (shown by double line) are atoms'X' and'Y'.

Let us draw perpendicular to the Y atom, which meets the unit cell at a point'Z' as shown in the figure, which is a distance of a/4.

3.  Coordination number:

We know that the coordination number is the nearest atoms (shown by double line) for Y atom is 4. Therefore the coordination number of diamond is 4

4. Atomic packing factor:

we know

Atomic packing factor(APF)=

volume occupied by the atoms per unit cell (v)/volume of the unit cell(V) --- > (1)

Substituting equations(2) and (3) in (1) we get

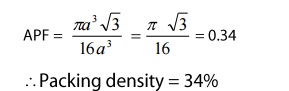
Thus we can say that 34% voulme of the unit cel in diamond cubic structure is occupied by the atoms and the remaining 66% volume is vacant.

Since the packing density is very low, it is termed as very loosely packed structure.

SODIUM CHLORIED STRUCTURE:

Ionic solids are made up of cat ion(+ion) and anions (-ion). Genrally, the cations (+ ve) are smaller in size to anions.

  Sodium choride and many other ionic crystals crystalline in rock slat structure which is also known as sodium chloride structure.

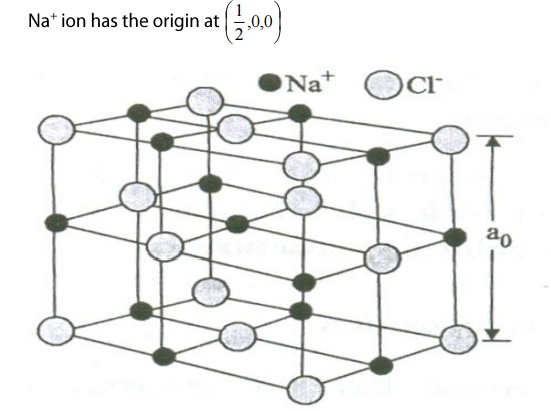
Structure compoition:

NaCl crystal has FCC structure with Na+ ion and cl ion as shown in the figure.

The Cl^- ions are situated at the corners as well as at the centers of the faces of the cube.  Na⁺ ions are situated exactly at the middle of the axial length of the unit cell along each axis.

          Thus NaCl crystal can be thought of as a compound of two FCC Na+ and

Cl sub lattices

       When one of the Cl ions has the origin at (0,0,0) then one of the nearest

Na⁺ ion has origin at (1/2,0,0)

Let us discuss the important parameters of the NaCl crystal.

     In NaCl structure, it has two types of ions namely, Na⁺ and Cl^- . Let us find the number of sodium ions separately.

a. Number of Na+ ions per unit cell

Na+ ion is located at the midpoint of the axial length. There are 12 such mid points Na+ ions. Each sodium ion is shared by 4 adfacent unit cell.

Share of one unit cell

Number of mid point Na+ ions per unit cell

¼ x 12 = 3 ions.

One sodium ion is located at the center of the unit cell.

Therefore, the number of sodium ions per unit cell = 3+1=4 ions

b. Number of Cl^- ions per unit cell

Here, there are two types of Cl^- ion namely Corner Cl ion and face centered Cl ion as shown in the figure.

There are 8 chlorine atoms in the corners and they are shared by 8 adjacent unit cells.

Number of corner Cl^-  ions per unit cell

= 1/8 x 8 1 ion.

Each face centered Cl^- ion is shared by 2 adjoining unit cell. There are 6 face centered Cl^- ions.

Number of face centered Cl^- ions per unit cell

= ½ x 6 = 3 ions.

Therefore total number of chlorine ions per unit cell = 1+3 = 4 ions.

Thus, there are 4 Na+ and 4Cl- ions per unit cell. That is total number of sodium and chlorine ions per unit cell are 8.

2.     Coordination number:

Each Na+ and 6 Cl- ions as nearest neighbors and similarly each Cl- ion has 6 Na+ ions has nearest neighbours. Hence, the coordination number of NaCl for opposite kind of ions is 6.

3.     Nearest neighbours distance

The nearest neighbor distance is a/2