Rotating Magnetic Field and Induced Voltages

Rotating Magnetic Field and Induced Voltages

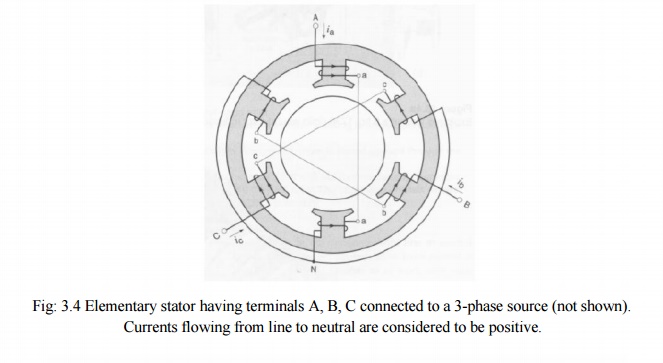
Consider a simple stator having 6 salient poles, each of which carries a coil having 5 turns (Fig.3.4). Coils that are diametrically opposite are connected in series by means of three jumpers that respectively connect terminals a-a, b-b, and c-c. This creates three identical sets of windings AN, BN, CN, which are mechanically spaced at 120 degrees to each other. The two coils in each winding produce magneto motive forces that act in the same direction.

The three sets of windings are connected in wye, thus forming a common neutral N. Owing to the perfectly symmetrical arrangement, the line to neutral impedances are identical. In other words, as regards terminals A, B, C, the windings constitute a balanced 3-phase system.

For a two-pole machine, rotating in the air gap, the magnetic field (i.e., flux density) being sinusoidally distributed with the peak along the centre of the magnetic poles. The result is illustrated in Fig.3.5. The rotating field will induce voltages in the phase coils aa', bb', and cc'. Expressions for the induced voltages can be obtained by using Faraday laws of induction.

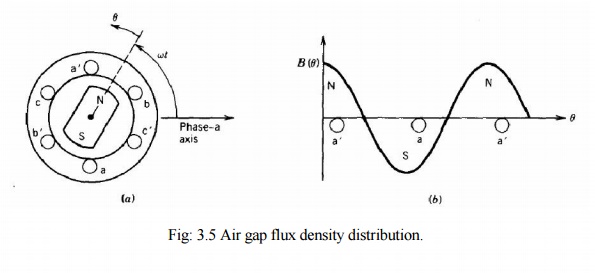
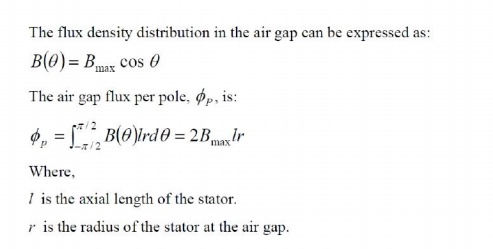
Let us consider that the phase coils are full-pitch coils of N turns (the coil sides of each phase are 180 electrical degrees apart as shown in Fig.3.5). It is obvious that as the rotating field moves (or the magnetic poles rotate) the flux linkage of a coil will vary. The flux linkage for coil aa' will be maximum.

Where f is the frequency in hertz. Above equation has the same form as that for the induced voltage in transformers. However, Ø_P represents the flux per pole of the machine.

The above equation also shows the rms voltage per phase. The N is the total number of series turns per phase with the turns forming a concentrated full-pitch winding. In an actual AC machine each phase winding is distributed in a number of slots for better use of the iron and copper and to improve the waveform. For such a distributed winding, the EMF induced in various coils placed in different slots are not in time phase, and therefore the phasor sum of the EMF is less than their numerical sum when they are connected in series for the phase winding. A reduction factor K_W, called the winding factor, must therefore be applied. For most three-phase machine windings K_W is about 0.85 to 0.95.

Therefore, for a distributed phase winding, the rms voltage per phase is

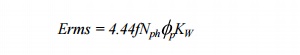
Where N_ph is the number of turns in series per phase.