Refraction of Light

Refraction of Light

We know that when a light ray falls on a polished surface placed in air, it is reflected into the air itself. When it falls on a transparent material, it is not reflected completely, but a part of it is reflected, a part of it is absorbed and most of the light passes through it. Through air, light travels with a speed of 3 × 10⁸ m s^-1, but it cannot travel with the same speed in water or glass, because, optically denser medium such as water and glass offer some resistance to the light rays.

So, light rays travelling from a rarer medium like air into a denser medium like glass or water are deviated from their straight line path. This bending of light about the normal, at the point of incidence; as it passes from one transparent medium to another is called refraction of light.

When a light ray travels from the rarer medium into the denser medium, it bends towards the normal and when it travels from the denser medium into the rarer medium, it bends away from the normal. You can observe this phenomenon with the help of the activity given below.

Activity 6

Take a glass beaker, fill it with water and place a pencil in it. Now, look at the pencil through the beaker. Does it appear straight? No. It will appear to be bent at the surface of the water. Why?

Answer:

Aim : To understand refraction of light.

Materials required : Glass beaker, water, pencil.

Procedure :

(i) Take a glass beaker.

(ii) Fill it with water

(iii) Place a pencil in it.

(iv) Now look at the pencil through the glass beaker.

(v) Does it appear straight?

Observation : It will appear to be bent at the surface of the water.

Inference :

The light rays actually travel from the water (a denser medium) into the air (a rarer medium).

(ii) When a light ray travels from a denser medium to a rarer medium, it is deviated from its straight line path.

(iii) So, the pencil appears to be bent when you see it through the glass of water.

(iv) Thus; the bending of light rays when it travels from one medium to another medium is called refraction. 

In this activity, the light rays actually travel from the water (a denser medium) into the air (a rarer medium). As you saw earlier, when a light ray travels from a denser medium to a rarer medium, it is deviated from its straight line path. So, the pencil appears to be bent when you see it through the glass of water.

1. Refractive Index

Refraction of light in a medium depends on the speed of light in that medium. When the speed of light in a medium is more, the bending is less and when the speed of light is less, the bending is more.

 The amount of refraction of light in a medium is denoted by a term known as refractive index of the medium, which is the ratio of the speed of light in the air to the speed of light in that particular medium. It is also known as the absolute refractive index and it is denoted by the Greek letter ‘µ’ (pronounced as ‘mew’).

μ = Speed of light in air (c) / Speed of light in the medium (v)

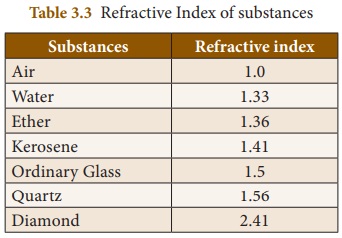
Refractive index is a ratio of two similar quantities (speed) and so, it has no unit. Since, the speed of light in any medium is less than its speed in air, refractive index of any transparent medium is always greater than 1. Refractive indices of some common substances are given in Table 3. 3.

In general, the refractive index of one medium with respect to another medium is given by the ratio of their absolute refractive indices.

1μ₂ = Absolve refractive index of the second medium / Absolve refractive index of the first medium

1μ₂ = [c/V₂] / [c/V₁]

Or

1μ₂ = V₁/ V₂

Thus, the refractive index of one medium with respect to another medium is also given by the ratio of the speed of light in the first medium to its speed in the second medium.

Problem 4

Speed of light in air is 3 × 10⁸ m s^-1 and the speed of light in a medium is 2 ×10⁸ ms^-1. Find the refractive index of the medium with respect to air.

Solution

Refractive index (μ) = Speed of light in air (c) / Speed of light in the medium (v)

μ = 3×10⁸ / 2×10⁸ = 1.5

Problem 5

Refractive index of water is 4/3 and the refractive index of glass is 3/2. Find the refractive index of glass with respect to the refractive index of water.

Solution

_wμ_g = Refractive index of glass / Refractive index of water

 = (3/2) / (4/3) = 9/8 = 1.125

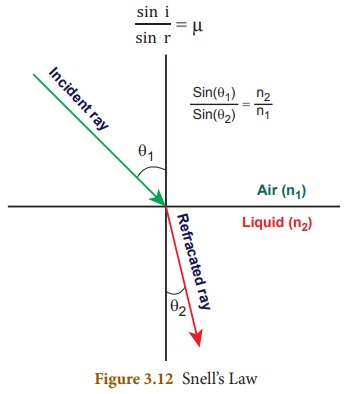
2. Snell’s Law of Refraction

Refraction of light rays, as they travel from one medium to another medium, obeys two laws, which are known as Snell’s laws of refraction. They are given below:

i)   The incident ray, the refracted ray and the normal at the point of intersection, all lie in the same plane.

ii) The ratio of the sine of the angle of incidence (i) to the sine of the angle of refraction (r) is equal to the refractive index of the medium, which is a constant.