Reduction Potentials in the Electron Transport Chain

Reduction Potentials in the Electron Transport Chain

Up until now, most of the energy considerations we have had concerned phosphorylation potentials. We saw how the free-energy change associated with hydrolysis of ATP could be used to drive otherwise endergonic reactions. The opposite is also true—when a reaction is highly exergonic, it can drive the formation of ATP. When we look closely at the energy changes in electron transport, a more useful approach is to consider the change in energy associated with the movement of electrons from one carrier to another. Each carrier in the electron transport chain can be isolated and studied, and each can exist in an oxidized or a reduced form. If we had two potential electron carriers, such as NADH and coenzyme Q, for example, how would we know whether electrons would be more likely to be transferred from the NADH to the coenzyme Q or the other way around? This is determined by measuring a reduction potential for each of the carriers. 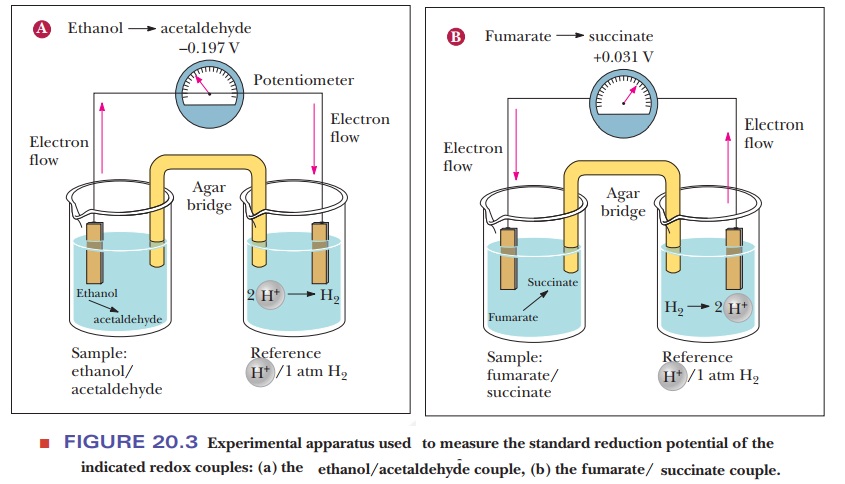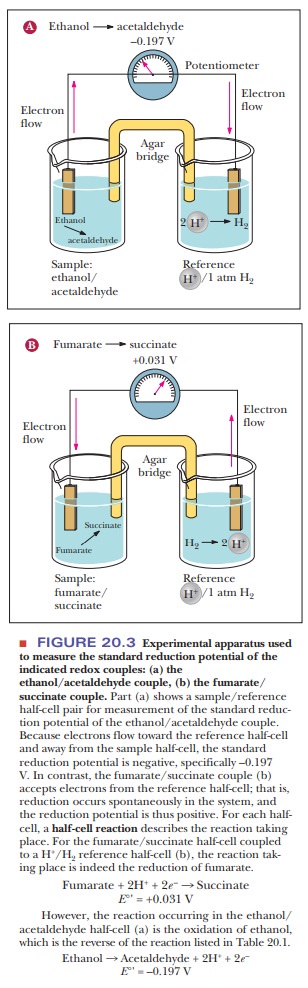A molecule with a high reduction potential tends to be reduced if it is paired with a molecule with a lower reduction potential. This is measured by making a simple battery cell, as shown in Figure 20.3. The reference point is the half-cell on the right where hydrogen ion is in aqueous solution in equilibrium with hydrogen gas. The reduction of hydrogen ion to hydrogen gas

2H⁺ + 2e^– - > H₂

is the control and is considered to have a voltage (E) of zero. The sample to be tested is in the other half-cell. The electric circuit is completed by bridge with a salt-containing agar gel.

How can reduction potentials be used to predict the direction of electron transport?

Figure 20.3a shows what happens if ethanol and acetaldehyde are put into the sample half-cell. Electrons flow away from the sample cell and toward the reference cell. This means that the hydrogen ion is being reduced to hydrogen gas and the ethanol is being oxidized to acetaldehyde. Therefore, the hydrogen/ H⁺ pair has a higher reduction potential than the ethanol/acetaldehyde pair. If we look at Figure 20.3b, we see the opposite. When fumarate and succinate are put into the sample half-cell, the electrons flow in the opposite direction, meaning that fumarate is being reduced to succinate while hydrogen gas is being oxidized to H⁺. The direction of electron flow and the magnitude of the observed voltage allow us to make a table, as shown in Table 20.1. Because this is a table of standard reduction potentials, all the reactions are shown as reductions. The value being measured is the standard biological voltage of each half reaction E°'. This value is calculated based on the compounds in the cells being at 1 M and the pH being 7 at the standard temperature of 25°C.

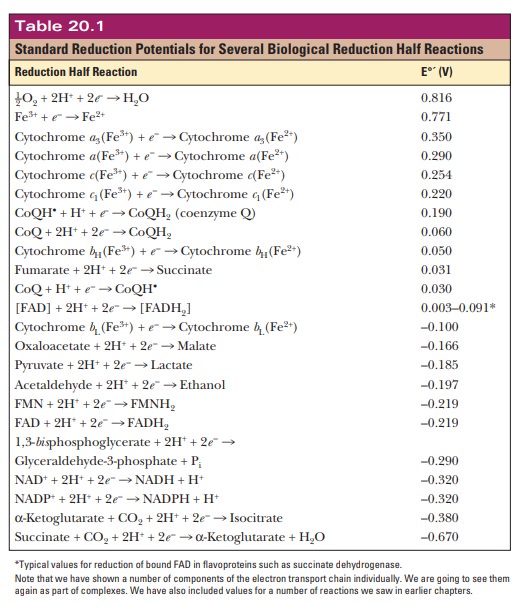
To interpret the data in this table for the purpose of electron transport, we need to look at the reduction potentials of the electron carriers involved. A reaction at the top of the table tends to occur as written if it is paired with a reaction that is lower down on the table. For example, we have already seen that the final step of the electron transport chain is the reduction of oxygen to water. This reaction is at the top of Table 20.1 with a reduction potential of 0.816 V, a very positive number. If this reaction were paired directly with NAD⁺/NADH, what would happen? The standard reduction potential for NAD⁺ forming NADH is given near the bottom of the table. Its reduction potential is –0.320 V.

NAD⁺ + 2H⁺ + 2e^– - > NADH + H⁺E°' = –0.320 V

This means that, if the two half reactions are paired during a redox reaction, the one for the NADH must be reversed. NADH gives up its electrons so that oxygen can be reduced to water:

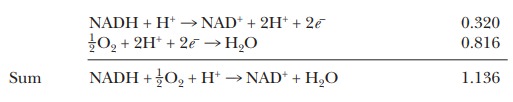
The overall voltage for this reaction is the sum of the standard reduction potentials—in this case, 0.816 V + 0.320 V, or 1.136 V. Note that we had to change the sign on the standard reduction potential for the NADH because we had to reverse the direction of its reaction.

The ∆G° of a redox reaction is calculated using

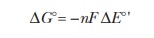
wheren is the number moles of electrons transferred, F is Faraday’s constant (96.485 kJ V^–1 mol^–1), and ΔΕ°' is the total voltage for the two half reactions. As we can see by this equation, ∆G° is negative when ΔΕ°' is positive. Therefore, we can always calculate the direction in which a redox reaction will go under standard conditions by combining the two half reactions in the way that gives the largest positive value for ΔΕ°'. For this example, ∆G° would be calculated as follows:

∆G° = –(2)(96.485 kJ V^–1mol^–1)(1.136 V) = –219 kJ mol^–1

This would be a very large number if NADH reduced oxygen directly. As we shall see in the next section, NADH passes its electrons along a chain that eventually leads to oxygen, but it does not reduce oxygen directly.

Before moving on, it should be noted that, just as there is a difference between ∆G° and ∆G, there is a similar difference between E° and E. Recall that we devoted several sections to the question of standard states, including the modified standard state for biochemical reactions. The notations G and E refer to the free-energy change and the reduction poten-tial under any conditions, respectively. When all components of a reaction are in their standard state (1 atm pressure, 25°C, all solutes at 1 M concentration), we write ∆G° and E°, respectively, for the standard free-energy change and standard reduction potential. The modified standard state for biochemical reactions takes note of the fact that having all solutes at 1 M concentration includes the hydrogen ion concentration. That implies a pH equal to zero. Consequently, we define a modified standard state for biochemistry that dif-fers from the usual one only in that pH = 7. Under these conditions, we write ∆G°’ and E°' for the standard free-energy change and the standard reductionpotential, respectively. The true direction of electron flow in a redox reaction is also based on the true values of the concentrations for the reactants and products, since the cellular concentrations are never 1 M.

Summary

Standard reduction potentials provide a basis for comparison among oxidation–reduction reactions.

The sequence of reactions in the electron transport chain can be pre-dicted by using reduction potentials.