Optimization of DFA-Based Pattern Matchers

Optimization of DFA-Based Pattern Matchers

1 Important States of an NFA

2 Functions Computed From the Syntax Tree

3 Computing unliable, firstpos, and lastpos

4 Computing followpos

5 Converting a Regular Expression Directly to a DFA

6 Minimizing the Number of States of a DFA

7 State Minimization in Lexical Analyzers

8 Trading Time for Space in DFA Simulation

In this section we present three algorithms that have been used to implement and optimize pattern matchers constructed from regular expressions.

                        The first algorithm is useful in a Lex compiler, because it constructs a DFA directly from a regular expression, without constructing an interme-diate NFA. The resulting DFA also may have fewer states than the DFA constructed via an NFA.

                        The second algorithm minimizes the number of states of any DFA, by combining states that have the same future behavior. The algorithm

itself is quite efficient, running in time 0(n log n), where n is the number of states of the DFA.

                        The third algorithm produces more compact representations of transition tables than the standard, two-dimensional table.

1. Important States of an NFA

To begin our discussion of how to go directly from a regular expression to a DFA, we must first dissect the NFA construction of Algorithm 3.23 and consider the roles played by various states. We call a state of an NFA important if it has a non-e out-transition. Notice that the subset construction (Algorithm 3.20) uses only the important states in a set T when it computes e-closure(move(T, a)), the set of states reachable from T on input a. That is, the set of states move(s, a) is nonempty only if state s is important. During the subset construction, two sets of NFA states can be identified (treated as if they were the same set) if they:

            Have the same important states, and

            Either both have accepting states or neither does.

            When the NFA is constructed from a regular expression by Algorithm 3.23, we can say more about the important states. The only important states are those introduced as initial states in the basis part for a particular symbol posi-tion in the regular expression. That is, each important state corresponds to a particular operand in the regular expression.

            The constructed NFA has only one accepting state, but this state, having no out-transitions, is not an important state. By concatenating a unique right endmarker # to a regular expression r, we give the accepting state for r a transition on #, making it an important state of the NFA for ( r ) # . In other words, by using the augmented regular expression ( r ) # , we can forget about accepting states as the subset construction proceeds; when the construction is complete, any state with a transition on # must be an accepting state.

            The important states of the NFA correspond directly to the positions in the regular expression that hold symbols of the alphabet. It is useful, as we shall see, to present the regular expression by its syntax tree, where the leaves correspond to operands and the interior nodes correspond to operators. An interior node is called a cat-node, or-node, or star-node if it is labeled by the concatenation operator (dot), union operator |, or star operator *, respectively. We can construct a syntax tree for a regular expression just as we did for arithmetic expressions in Section 2.5.1.

Example 3.31 : Figure 3.56 shows the syntax tree for the regular expression of our running example. Cat-nodes are represented by circles. •

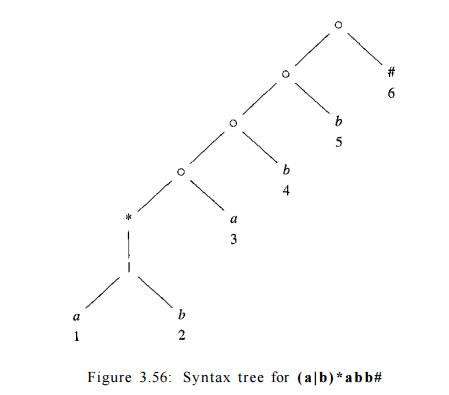
Leaves in a syntax tree are labeled by e or by an alphabet symbol. To each leaf not labeled e, we attach a unique integer. We refer to this integer as the position of the leaf and also as a position of its symbol. Note that a symbol can have several positions; for instance, a has positions 1 and 3 in Fig. 3.56. The positions in the syntax tree correspond to the important states of the constructed NFA.

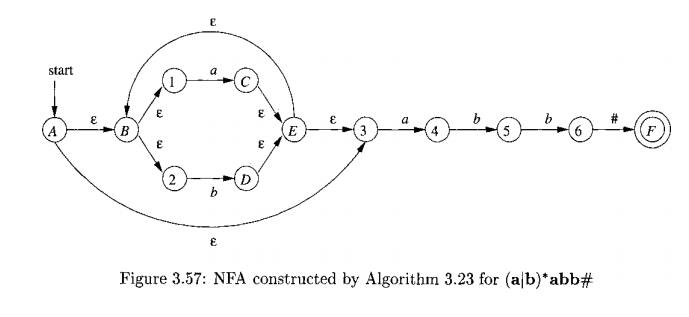
Example 3.32 : Figure 3.57 shows the NFA for the same regular expression as Fig. 3.56, with the important states numbered and other states represented by letters. The numbered states in the NFA and the positions in the syntax tree correspond in a way we shall soon see. •

2. Functions Computed From the Syntax Tree

To construct a DFA directly from a regular expression, we construct its syntax tree and then compute four functions: nullable, firstpos, lastpos, and followpos, defined as follows. Each definition refers to the syntax tree for a particular augmented regular expression ( r ) # .

1. nullable(n) is true for a syntax-tree node n if and only if the subexpression represented by n has e in its language. That is, the subexpression can be "made null" or the empty string, even though there may be other strings it can represent as well.

2. firstpos(n) is the set of positions in the subtree rooted at n that corre-spond to the first symbol of at least one string in the language of the subexpression rooted at n.

3. lastpos(n) is the set of positions in the subtree rooted at n that corre-spond to the last symbol of at least one string in the language of the subexpression rooted at n.

4. followpos(p), for a position p, is the set of positions q in the entire syntax tree such that there is some string x = axa2 ••• an in L ( ( r ) # ) such that for some i, there is a way to explain the membership of x in L ( ( r ) # ) by matching to position p of the syntax tree and ai+i to position g.

Example 3.33 : Consider the cat-node n in Fig. 3.56 that corresponds to the expression (a|b)*a. We claim nullable(ri) is false, since this node generates all strings of a's and 6's ending in an a; it does not generate e. On the other hand, the star-node below it is nullable; it generates e along with all other strings of a's and 6's.

firstpos{n) — {1,2,3} . In a typical generated string like aa, the first position of the string corresponds to position 1 of the tree, and in a string like 6a, the first position of the string comes from position 2 of the tree. However, when the string generated by the expression of node n is just a, then this a comes from position 3.

lastpos{n) — {3}. That is, no matter what string is generated from the expression of node n, the last position is the a from position 3 of the tree.

followpos is trickier to compute, but we shall see the rules for doing so shortly. Here is an example of the reasoning: followpos(l) — {1,2,3} . Consider a string • • • ac • • •, where the c is either a or 6, and the a comes from position 1. That is, this a is one of those generated by the a in expression (a|b)*. This a could be followed by another a or 6 coming from the same subexpression, in which case c comes from position 1 or 2. It is also possible that this a is the last in the string generated by (a|b)*, in which case the symbol c must be the a that comes from position 3. Thus, 1,2, and 3 are exactly the positions that can follow position 1. • • . '

3 Computing nullable, firstpos, and lastpos

We can compute nullable, firstpos, and lastpos by a straightforward recursion on the height of the tree. The basis and inductive rules for nullable and firstpos are summarized in Fig. 3.58. The rules for lastpos are essentially the same as for firstpos, but the roles of children c\ and c2 must be swapped in the rule for a cat-node.

Example 3 . 3 4 : Of all the nodes in Fig. 3.56 only the star-node is nullable. We note from the table of Fig. 3.58 that none of the leaves are nullable, because they each correspond to non-e operands. The or-node is not nullable, because neither of its children is. The star-node is nullable, because every star-node is nullable. Finally, each of the cat-nodes, having at least one nonnullable child, is not nullable.

The computation of firstpos and lastpos for each of the nodes is shown in

Fig. 3.59, with firstposin) to the left of node n, and lastpos(n) to its right. Each of the leaves has only itself for firstpos and lastpos, as required by the rule for non-e leaves in Fig. 3.58. For the or-node, we take the union of firstpos at the

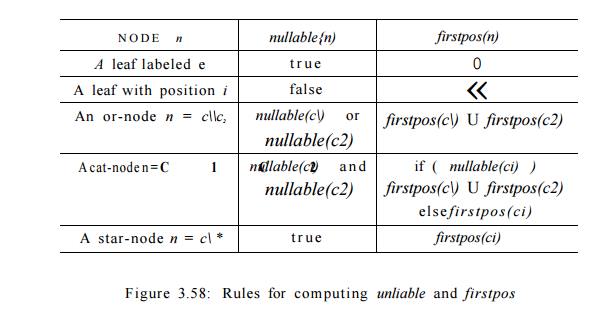
children and do the same for lastpos. The rule for the star-node says that we take the value of firstpos or lastpos at the one child of that node.

Now, consider the lowest cat-node, which we shall call n. To compute firstpos(n), we first consider whether the left operand is mailable, which it is in this case. Therefore, firstpos for n is the union of firstpos for each of its children, that is {1,2} U {3} = {1,2,3} . The rule for lastpos does not appear explicitly in Fig. 3.58, but as we mentioned, the rules are the same as for firstpos, with the children interchanged. That is, to compute lastpos(n) we must ask whether its right child (the leaf with position 3) is nullable, which it is not. Therefore, lastpos(n) is the same as lastpos of the right child, or {3}.

4 Computing followpos

Finally, we need to see how to compute followpos. There are only two ways that a position of a regular expression can be made to follow another.

1 . I f n i s a cat-node with left child c \ and right child C 2 , then for every position i  in  lastpos(ci),  all positions in firstpos(c2) are in followpos(i).

2. If n is a star-node, and i is a position in lastpos(n), then all positions in firstpos(n) are in followpos(i).

E x a m p l e 3.35 : Let us continue with our running example; recall that firstpos and lastpos were computed in Fig. 3.59. Rule 1 for followpos requires that we look at each cat-node, and put each position in firstpos of its right child in followpos for each position in lastpos of its left child. For the lowest cat-node in Fig. 3.59, that rule says position 3 is in followpos(l) and followpos{2). The next cat-node above says that 4 is in followpos(2>), and the remaining two cat-nodes give us 5 in followpos(4) and 6 in followpos(5).

Figure 3.59: firstpos and lastpos for nodes in the syntax tree for (a|b)*abb#

We must also apply rule 2 to the star-node. That rule tells us positions 1 and 2 are in both followpos(l) and followpos(2), since both firstpos and lastpos for this node are {1,2} . The complete sets followpos are summarized in Fig. 3.60.

We can represent the function followpos by creating a directed graph with a node for each position and an arc from position i to position j if and only if j is in followpos(i). Figure 3.61 shows this graph for the function of Fig. 3.60.

It should come as no surprise that the graph for followpos is almost an NFA without e-transitions for the underlying regular expression, and would become one if we:

1. Make all positions in firstpos of the root be initial states,

2. Label each arc from i to j by the symbol at position i, and

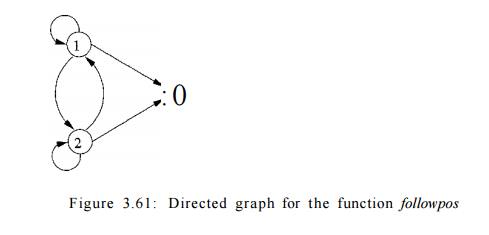
3.  Make the position associated with endmarker  #  be the only accepting state.

5. Converting a Regular Expression Directly to a DFA

Algorithm 3.36 : Construction of a DFA from a regular expression r.

INPUT : A regular expression r.

OUTPUT : A DFA D that recognizes L(r).

METHOD :

1. Construct a syntax tree T from the augmented regular expression ( r ) # .

2. Compute nullable, firstpos, lastpos, and followpos for T, using the methods of Sections 3.9.3 and 3.9.4.

 Construct Dstates, the set of states of DFA D, and Dtran, the transition function for D, by the procedure of Fig. 3.62. The states of D are sets of

positions in T. Initially, each state is "unmarked," and a state becomes "marked" just before we consider its out-transitions. The start state of D is firstpos(no), where node no is the root of T. The accepting states are those containing the position for the endmarker symbol #. •

Example 3.37 : We can now put together the steps of our running example to construct a DFA for the regular expression r = (a|b)*abb. The syntax tree for ( r ) # appeared in Fig. 3.56. We observed that for this tree, nullable is true only for the star-node, and we exhibited firstpos and lastpos in Fig. 3.59. The values of followpos appear in Fig. 3.60.

The value of firstpos for the root of the tree is {1,2,3}, so this set is the start state of D. Call this set of states A. We must compute Dtran[A, a] and Dtran[A, b]. Among the positions of A, 1 and 3 correspond to a, while 2 corresponds to b. Thus, Dtran[A,a] = followpos(l) U followpos(3) = {1,2,3,4},

initialize Dstates to contain only the unmarked state firstpos(no), where no is the root of syntax tree T for ( r ) # ;

w h i le ( there is an unmarked state S in Dstates )  {

mark  S;

for ( each input symbol a ) {

let  U be the union of followpos(p)  for all p

in S that correspond to a;

if ( U is not in Dstates )

add U as an unmarked state to Dstates; Dtran[S, a) = U;

}

}

Figure 3.62:  Construction of a DFA directly from a regular expression

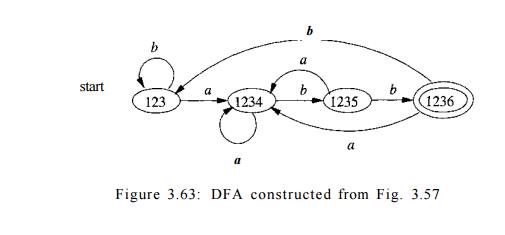
and Dtran[A, b] = followpos{2) = {1,2,3} . The latter is state A, and so does not have to be added to Dstates, but the former, B = {1,2,3,4}, is new, so we add it to Dstates and proceed to compute its transitions. The complete DFA is shown in Fig. 3.63. •

6. Minimizing the Number of States of a DFA

There can be many DFA's that recognize the same language. For instance, note that the DFA's of Figs. 3.36 and 3.63 both recognize language L ( ( a | b ) * a b b ) . Not only do these automata have states with different names, but they don't even have the same number of states. If we implement a lexical analyzer as a DFA, we would generally prefer a DFA with as few states as possible, since each state requires entries in the table that describes the lexical analyzer.

The matter of the names of states is minor. We shall say that two automata are the same up to state names if one can be transformed into the other by doing nothing more than changing the names of states. Figures 3.36 and 3.63 are not the same up to state names. However, there is a close relationship between the states of each. States A and C of Fig. 3.36 are actually equivalent, in the sense that neither is an accepting state, and on any input they transfer to the same state — to B on input a and to C on input b. Moreover, both states A and C behave like state 123 of Fig. 3.63. Likewise, state B of Fig. 3.36 behaves like state 1234 of Fig. 3.63, state D behaves like state 1235, and state E behaves like state 1236.

It turns out that there is always a unique (up to state names) minimum state DFA for any regular language. Moreover, this minimum-state DFA can be constructed from any DFA for the same language by grouping sets of equivalent states. In the case of L ( ( a | b ) * a b b ) , Fig. 3.63 is the minimum-state DFA, and it can be constructed by partitioning the states of Fig. 3.36 as {A, C}{B}{D}{E}.

In order to understand the algorithm for creating the partition of states that converts any DFA into its minimum-state equivalent DFA, we need to see how input strings distinguish states from one another. We say that string x distinguishes state s from state t if exactly one of the states reached from s and t by following the path with label x is an accepting state. State s is distinguishable from state t if there is some string that distinguishes them.

Example 3.38 : The empty string distinguishes any accepting state from any nonaccepting state. In Fig. 3.36, the string bb distinguishes state A from state B, since bb takes A to a nonaccepting state C, but takes B to accepting state •

The state-minimization algorithm works by partitioning the states of a DFA into groups of states that cannot be distinguished. Each group of states is then merged into a single state of the minimum-state DFA. The algorithm works by maintaining a partition, whose groups are sets of states that have not yet been distinguished, while any two states from different groups are known to be distinguishable. When the partition cannot be refined further by breaking any group into smaller groups, we have the minimum-state DFA.

Initially, the partition consists of two groups: the accepting states and the nonaccepting states. The fundamental step is to take some group of the current partition, say A = {si, s ₂ , . . . , s_k}, and some input symbol a, and see whether a can be used to distinguish between any states in group A. We examine the transitions from each of si, s₂,... , on input a, and if the states reached fall into two or more groups of the current partition, we split A into a collection of groups, so that si and Sj are in the same group if and only if they go to the same group on input a. We repeat this process of splitting groups, until for no group, and for no input symbol, can the group be split further. The idea is formalized in the next algorithm.

Algorithm 3 . 3 9 :  Minimizing the number of states of a DFA.

INPUT : A DFA D with set of states 5, input alphabet S, state state s ₀ , and set of accepting states F.

OUTPUT : A DFA D' accepting the same language as D and having as few states as possible.

Why the State-Minimization Algorithm Works

We need to prove two things:  that states remaining in the same group in

Hfinal are indistinguishable by any string, and that states winding up in

different groups are distinguishable. The first is an induction on i that if after the ith iteration of step (2) of Algorithm 3.39, s and t are in the same group, then there is no string of length i or less that distinguishes them. We shall leave the details of the induction to you.

The second is an induction on i that if states s and t are placed in different groups at the ith iteration of step (2), then there is a string that distinguishes them. The basis, when s and t are placed in different groups of the initial partition, is easy: one must be accepting and the other not, so e distinguishes them. For the induction, there must be an input a and states p and q such that s and t go to states p and q, respectively, on input a. Moreover, p and q must already have been placed in different groups. Then by the inductive hypothesis, there is some string x that distinguishes

p from q.  Therefore, ax distinguishes s from t.

M E T H O D :

1. Start with an initial partition II with two groups, F and S — F, the accepting and nonaccepting states of D.

2. Apply the procedure of Fig. 3 . 64 to construct a new partition n new initially, let llnew = II;

 for ( each group G of U ) {

 partition G into subgroups such that two states s and t are in the same subgroup if and only if for all input symbols a, states s and t have transitions on a to states in the same group of Tl;

 /* at worst, a state will be in a subgroup by itself */

 replace G in nn e w by the set of all subgroups formed;

 }

 Figure 3.64: Construction of nn ew

3 . If nn e w = FT, let llflnai = II and continue with step (4). Otherwise, repeat step (2) with Ilnew in place of Tl.

4. Choose one state in each group of IIfin a i as the representative for that group. The representatives will be the states of the minimum-state DFA D'. The other components of D' are constructed as follows:

Eliminating the Dead State

T he minimization algorithm sometimes produces a DFA with one dead state — one that is not accepting and transfers to itself on each input symbol. This state is technically needed, because a DFA must have a transition from every state on every symbol. However, as discussed in Section 3.8.3, we often want to know when there is no longer any possibility of acceptance, so we can establish that the proper lexeme has already been seen. Thus, we may wish to eliminate the dead state and use an automaton that is missing some transitions. This automaton has one fewer state than the minimum-state DFA, but is strictly speaking not a DFA, because of the missing transitions to the dead state.

(a) The state state of D' is the representative of the group containing the start state of D.

 The accepting states of D' are the representatives of those groups that contain an accepting state of D. Note that each group contains either only accepting states, or only nonaccepting states, because we started by separating those two classes of states, and the procedure of Fig. 3.64 always forms new groups that are subgroups of previously constructed groups.

 Let s be the representative of some group G of nfin a i, and let the transition of D from s on input a be to state t. Let r be the representative of fs group H. Then in D', there is a transition from s to r on input a. Note that in D, every state in group G must go to some state of group H on input a, or else, group G would have been split according to Fig. 3.64.

Example 3.40 : Let us reconsider the DFA of Fig. 3.36. The initial partition consists of the two groups {A, B, C, D}{E}, which are respectively the nonaccepting states and the accepting states. To construct n n e w 5 the procedure of Fig. 3.64 considers both groups and inputs a and b. The group {E} cannot be split, because it has only one state, so {E} will remain intact in n n e w -

The other group {A, B:C,D} can be split, so we must consider the effect of each input symbol. On input a, each of these states goes to state B, so there is no way to distinguish these states using strings that begin with a. On input 6, states A, 5, and C go to members of group {A, B, C, D}: while state D goes to E, a member of another group. Thus, in n n e w , group {A, B,C, D} is split into {A,B,C}{D}, and n n e w for this round is {A,B,C}{D}{E}.

In the next round, we can split {A,B,C} into {A,C}{B}, since A and C each go to a member of {A, B, C} on input b, while B goes to a member of another group, {D}. Thus, after the second round, nn e w = {A, C}{B}{D}{E}. For the third round, we cannot split the one remaining group with more than one state, since A and C each go to the same state (and therefore to the same group) on each input. We conclude that Ilfin a i = {A, C}{B}{D}{E}.

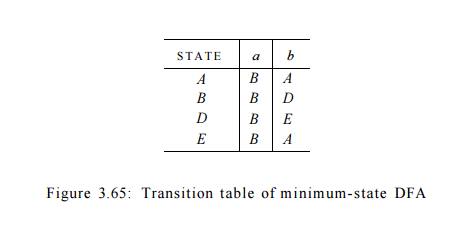
Now, we shall construct the minimum-state DFA. It has four states, corre-sponding to the four groups of Ufina\, and let us pick A, B, D, and E as the representatives of these groups. The initial state is A, and the only accepting state is E. Figure 3.65 shows the transition function for the DFA. For instance, the transition from state E on input b is to A, since in the original DFA, E goes to C on input 6, and A is the representative of C's group. For the same reason, the transition on b from state A is to A itself, while all other transitions are as in Fig. 3.36. •

7. State Minimization in Lexical Analyzers

To apply the state minimization procedure to the DFA's generated in Sec-tion 3.8.3, we must begin Algorithm 3.39 with the partition that groups to-gether all states that recognize a particular token, and also places in one group all those states that do not indicate any token. An example should make the extension clear.

E x a m p l e 3 . 4 1 : For the DFA of Fig. 3.54, the initial partition is

{0137,7}{247}{8,58}{7}{68}{0}

That is, states 0137 and 7 belong together because neither announces any token. States 8 and 58 belong together because they both announce token a * b ⁺ . Note that we have added a dead state 0, which we suppose has transitions to itself on inputs a and b. The dead state is also the target of missing transitions on a from states 8, 58, and 68.

We must split 0137 from 7, because they go to different groups on input a. We also split 8 from 58, because they go to different groups on b. Thus, all states are in groups by themselves, and Fig. 3.54 is the minimum-state DFA recognizing its three tokens. Recall that a DFA serving as a lexical analyzer will normally drop the dead state, while we treat missing transitions as a signal to end token recognition. •

8. Trading Time for Space in DFA Simulation

The simplest and fastest way to represent the transition function of a DFA is a two-dimensional table indexed by states and characters. Given a state and next input character, we access the array to find the next state and any special action we must take, e.g., returning a token to the parser. Since a typical lexical analyzer has several hundred states in its DFA and involves the ASCII alphabet of 128 input characters, the array consumes less than a megabyte.

However, compilers are also appearing in very small devices, where even a megabyte of storage may be too much. For such situations, there are many methods that can be used to compact the transition table. For instance, we can represent each state by a list of transitions — that is, character-state pairs — ended by a default state that is to be chosen for any input character not on the list. If we choose as the default the most frequently occurring next state, we can often reduce the amount of storage needed by a large factor.

There is a more subtle data structure that allows us to combine the speed of array access with the compression of lists with defaults. We may think of this structure as four arrays, as suggested in Fig. 3.66.⁵ The base array is used to determine the base location of the entries for state s, which are located in the next and check arrays. The default array is used to determine an alternative base location if the check array tells us the one given by base[s] is invalid.

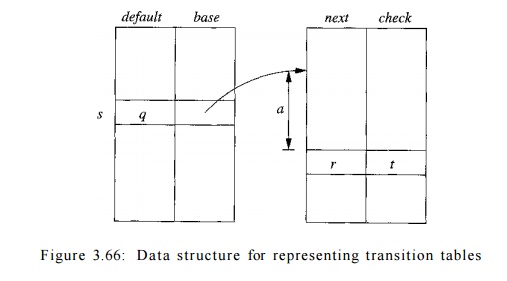
To compute nextState(s, a), the transition for state s on input a, we examine the next and check entries in location I = base[s]+a, where character o is treated as an integer, presumably in the range 0 to 127. If check[l) = s, then this entry

⁵ I n practice, there would be another array indexed by states to give the action associated with that state, if any.

is valid, and the next state for state s on input a is next[l]. If check[l] ^ s, then we determine another state t = defaults] and repeat the process as if t were the current state. More formally, the function nextState is defined as follows:

int nextState(s,a) {

if ( check[base[s] + a] = s ) r e t u r n next[base[s] + a];

else return nextState(default[s],a);

} 

The intended use of the structure of Fig. 3.66 is to make the next-check arrays short by taking advantage of the similarities among states. For instance, state t, the default for state s, might be the state that says "we are working on an identifier," like state 10 in Fig. 3.14. Perhaps state s is entered after seeing the letters t h , which are a prefix of keyword t h e n as well as potentially being the prefix of some lexeme for an identifier. On input character e, we must go from state s to a special state that remembers we have seen t h e , but otherwise, state s behaves as t does. Thus, we set check[base[s] + e] to s (to confirm that this entry is valid for s) and we set next[base[s] + e] to the state that remembers the . Also, default[s] is set to t.

While we may not be able to choose base values so that no next-check entries remain unused, experience has shown that the simple strategy of assigning base values to states in turn, and assigning each base[s] value the lowest integer so that the special entries for state s are not previously occupied utilizes little more space than the minimum possible.

Exercises for Section 3.9

Exercise 3 . 9 . 1 : Extend the table of Fig. 3.58 to include the operators (a) ? and (b) + .

Exercise 3 . 9 . 2 : Use Algorithm 3.36 to convert the regular expressions of Exercise 3.7.3 directly to deterministic finite automata .

Exercise 3 . 9 . 3 : We can prove that two regular expressions are equivalent by showing that their minimum-state DFA's are the same up to renaming of states. Show in this way that the following regular expressions: (a|b)*, (a*|b*)*, and ((e|a)b*)* are all equivalent. Note: You may have constructed the DFA's for these expressions in response to Exercise 3.7.3.

! Exercise 3 . 9 . 4 : Construct the minimum-state DFA's for the following regular expressions: 

(a|b)*a(a|b) .

(a|b)*a(a|b)(a|b) .

(a|b)*a(a|b)(a|b)(a|b) .

Do you see a pattern?

!! Exercise 3 . 9 . 5 : To make formal the informal claim of Example 3.25, show that any deterministic finite automaton for the regular expression

( a | b ) * a ( a | b ) ( a | b ) . . . ( a | b )