Design of a Lexical-Analyzer Generator

Design of a Lexical-Analyzer Generator

1 The Structure of the Generated Analyzer

2 Pattern Matching Based on NFA's

3 DFA's for Lexical Analyzers

4 Implementing the Lookahead Operator

5 Exercises for Section 3.8

In this section we shall apply the techniques presented in Section 3.7 to see how a lexical-analyzer generator such as Lex is architected. We discuss two approaches, based on NFA's and DFA's; the latter is essentially the implemen-tation of Lex.

1. The Structure of the Generated Analyzer

Figure 3.49 Overviews the architecture of a lexical analyzer generated by Lex. The program that serves as the lexical analyzer includes a fixed program that simulates an automaton; at this point we leave open whether that automaton is deterministic or nondeterministic. The rest of the lexical analyzer consists of components that are created from the Lex program by Lex itself.

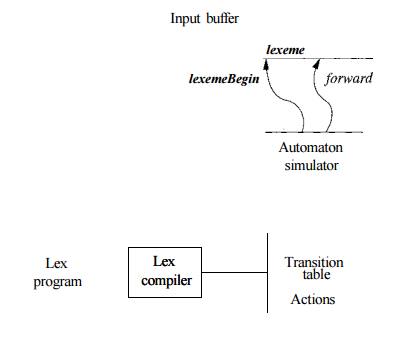
Figure 3.49: A Lex program is turned into a transition table and actions, which are used by a finite-automaton simulator

These components are:

            A transition table for the automaton.

            Those functions that are passed directly through Lex to the output (see Section 3.5.2).

                  The actions from the input program, which appear as fragments of code to be invoked at the appropriate time by the automaton simulator.

To construct the automaton, we begin by taking each regular-expression pattern in the Lex program and converting it, using Algorithm 3.23, to an NFA. We need a single automaton that will recognize lexemes matching any of the patterns in the program, so we combine all the NFA's into one by introducing a new start state with e-transitions to each of the start states of the NFA's N{ for pattern pi. This construction is shown in Fig. 3.50.

Example 3 . 2 6 : We shall illustrate the ideas of this section with the following simple, abstract example:

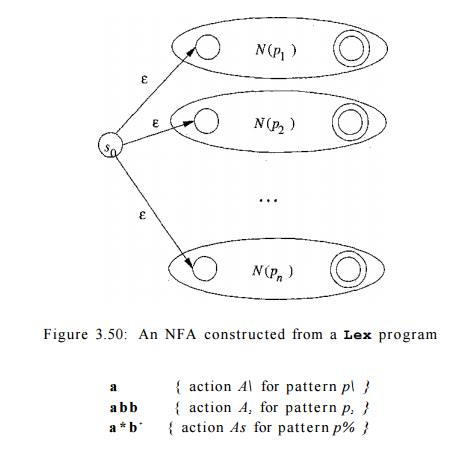
Note that  these  three  patterns  present  some  conflicts       of the type  discussed in Section 3.5.3. In particular, string abb matches both the second and third patterns, but we shall consider it a lexeme for pattern p2, since that pattern is listed first in the above Lex program. Then, input strings such as aabbb • • •

have many prefixes that match the third pattern. The Lex rule is to take the longest, so we continue reading 6's, until another a is met, whereupon we report the lexeme to be the initial a's followed by as many 6's as there are.

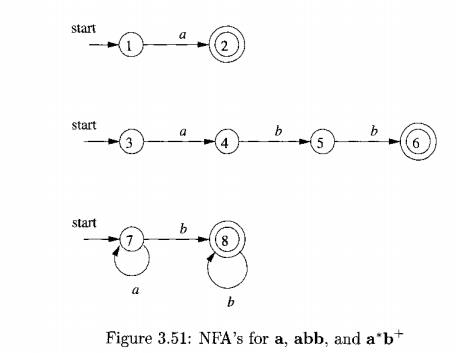
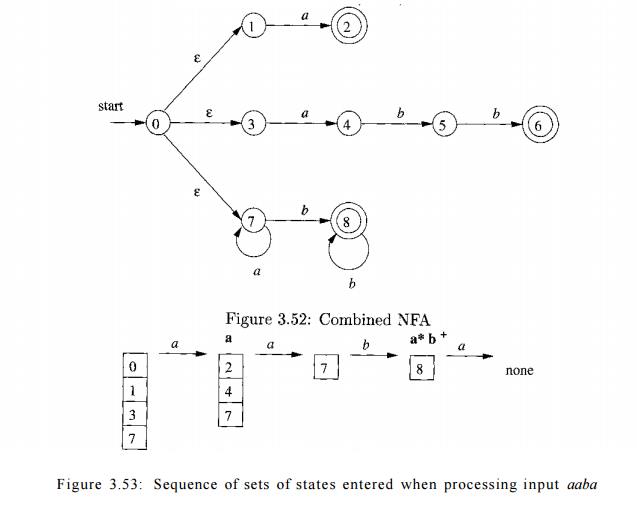
Figure 3.51 shows three NFA's that recognize the three patterns. The third is a simplification of what would come out of Algorithm 3.23. Then, Fig. 3.52 shows these three NFA's combined into a single NFA by the addition of start state 0 and three e-transitions. •

2. Pattern Matching Based on NFA's

If the lexical analyzer simulates an NFA such as that of Fig. 3.52, then it must read input beginning at the point on its input which we have referred to as lexemeBegin. As it moves the pointer called forward ahead in the input, it calculates the set of states it is in at each point, following Algorithm 3.22.

Eventually, the NFA simulation reaches a point on the input where there are no next states. At that point, there is no hope that any longer prefix of the input would ever get the NFA to an accepting state; rather, the set of states will always be empty. Thus, we are ready to decide on the longest prefix that is a lexeme matching some pattern.

We look backwards in the sequence of sets of states, until we find a set that includes one or more accepting states. If there are several accepting states in that set, pick the one associated with the earliest pattern pi in the list from the Lex program. Move the forward pointer back to the end of the lexeme, and perform the action Ai associated with pattern pi.

Example 3 . 27: Suppose we have the patterns of Example 3.26 and the input begins aaba. Figure 3.53 shows the sets of states of the NFA of Fig. 3.52 that we enter, starting with e-closure of the initial state 0, which is {0,1,3,7}, and proceeding from there. After reading the fourth input symbol, we are in an empty set of states, since in Fig. 3.52, there are no transitions out of state 8 on input a.

Thus, we need to back up, looking for a set of states that includes an accepting state. Notice that, as indicated in Fig. 3.53, after reading a we are in a set that includes state 2 and therefore indicates that the pattern a has been matched. However, after reading aab, we are in state 8, which indicates that a * b + has been matched; prefix aab is the longest prefix that gets us to an accepting state. We therefore select aab as the lexeme, and execute action A3, which should include a return to the parser indicating that the token whose pattern is p3 = a * b + has been found. •

3. DFA's for Lexical Analyzers

Another architecture, resembling the output of Lex, is to convert the NFA for all the patterns into an equivalent DFA, using the subset construction of Algorithm 3.20. Within each DFA state, if there are one or more accepting NFA states, determine the first pattern whose accepting state is represented, and make that pattern the output of the DFA state.

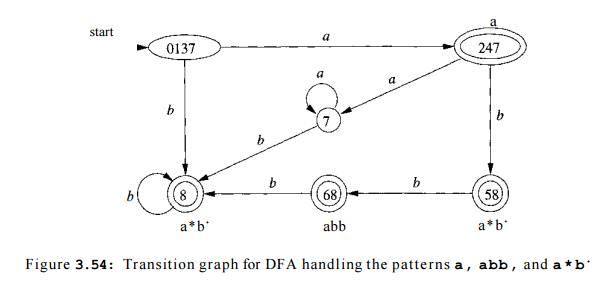
Example 3 . 2 8 : Figure 3.54 shows a transition diagram based on the DFA that is constructed by the subset construction from the NFA in Fig. 3.52. The accepting states are labeled by the pattern that is identified by that state. For instance, the state {6,8} has two accepting states, corresponding to patterns abb and a * b ⁺ . Since the former is listed first, that is the pattern associated with state {6,8} . •

We use the DFA in a lexical analyzer much as we did the NFA. We simulate the DFA until at some point there is no next state (or strictly speaking, the next state is 0, the dead state corresponding to the empty set of NFA states). At that point, we back up through the sequence of states we entered and, as soon as we meet an accepting DFA state, we perform the action associated with the pattern for that state.

Example 3 . 2 9 : Suppose the DFA of Fig. 3.54 is given input abba. The se-quence of states entered is 0137,247,58,68, and at the final a there is no tran-sition out of state 68. Thus, we consider the sequence from the end, and in this case, 68 itself is an accepting state that reports pattern p₂ = abb . •

4. Implementing the Lookahead Operator

Recall from Section 3.5.4 that the Lex lookahead operator / in a Lex pattern r\/r₂ is sometimes necessary, because the pattern r*i for a particular token may need to describe some trailing context r₂ in order to correctly identify the actual lexeme. When converting the pattern r\/r₂ to an NFA, we treat the / as if it were e, so we do not actually look for a / on the input. However, if the NFA recognizes a prefix xy of the input buffer as matching this regular expression, the end of the lexeme is not where the NFA entered its accepting state. Rather the end occurs when the NFA enters a state s such that

1. s has an e-transition on the (imaginary) /,

2.  There is a path from the start state of the NFA to state s that spells out x.

3. There is a path from state s to the accepting state that spells out y.

4. x is as long as possible for any xy satisfying conditions 1-3.

If there is only one e-transition state on the imaginary / in the NFA, then the end of the lexeme occurs when this state is entered for the last time as the following example illustrates. If the NFA has more than one e-transition state on the imaginary /, then the general problem of finding the correct state s is much more difficult.

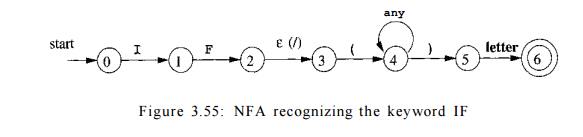
Example 3.30: An NFA for the pattern for the Fortran IF with lookahead, from Example 3.13, is shown in Fig. 3.55. Notice that the e-transition from state 2 to state 3 represents the lookahead operator. State 6 indicates the pres-ence of the keyword IF. However, we find the lexeme IF by scanning backwards to the last occurrence of state 2, whenever state 6 is entered. •

Dead States in DFA's

Technically, the automaton in Fig. 3.54 is not quite a DFA. The reason is that a DFA has a transition from every state on every input symbol in its input alphabet. Here, we have omitted transitions to the dead state 0, and we have therefore omitted the transitions from the dead state to itself on every input. Previous NFA-to-DFA examples did not have a way to get from the start state to 0, but the NFA of Fig. 3.52 does.

However, when we construct a DFA for use in a lexical analyzer, it is important that we treat the dead state differently, since we must know when there is no longer any possibility of recognizing a longer lexeme. Thus, we suggest always omitting transitions to the dead state and elimi-nating the dead state itself. In fact, the problem is harder than it appears, since an NFA-to-DFA construction may yield several states that cannot reach any accepting state, and we must know when any of these states have been reached. Section 3.9.6 discusses how to combine all these states into one dead state, so their identification becomes easy. It is also inter-esting to note that if we construct a DFA from a regular expression using Algorithms 3.20 and 3.23, then the DFA will not have any states besides 0 that cannot lead to an accepting state.

5. Exercises for Section 3.8

Exercise 3 . 8 . 1 : Suppose we have two tokens: (1) the keyword if, and (2) id-entifiers, which are strings of letters other than if. Show:

                 The NFA for these tokens, and

                 The DFA for these tokens.

Exercise 3.8.2 : Repeat Exercise 3.8.1 for tokens consisting of (1) the keyword while, (2) the keyword when, and (3) identifiers consisting of strings of letters and digits, beginning with a letter.

! Exercise 3 . 8 . 3 : Suppose we were to revise the definition of a DFA to allow zero or one transition out of each state on each input symbol (rather than exactly one such transition, as in the standard DFA definition). Some regular

expressions would then have smaller "DFA's" than they do under the standard definition of a DFA. Give an example of one such regular expression.

!! Exercise 3.8.4 :  Design    an algorithm to recognize Lex-lookahead patterns of the form r i / r 2 ,      where r\     and r2    are regular expressions.  Show how your algorithm works on the following inputs:

          (abcd\abc)jd

          (a\ab)/ba

!        aa * j a*