Chapter: Compilers : Principles, Techniques, & Tools : Lexical Analysis
Specification of Tokens
Specification of Tokens
1 Strings and Languages
2 Operations on Languages
3 Regular Expressions
4 Regular Definitions
5 Extensions of Regular
Expressions
6 Exercises for Section 3.3
Regular expressions are an important notation for specifying lexeme
patterns. While they cannot express all possible patterns, they are very
effective in spec ifying those types of patterns that we actually need for
tokens. In this section we shall study the formal notation for regular
expressions, and in Section 3.5 we shall see how these expressions are used in
a lexical-analyzer generator. Then, Section 3.7 shows how to build the lexical
analyzer by converting regular expressions to automata that perform the
recognition of the specified tokens.
Can We Run Out of Buffer Space?
In most modern languages, lexemes are short, and one or two characters
of lookahead is sufficient. Thus a buffer size N in the thousands is ample, and the double-buffer scheme of
Section 3.2.1 works without problem. However, there are some risks. For example, if
character strings can be very long, extending over many lines, then we could
face the possibility that a lexeme is longer than N. To avoid problems with long character strings, we can treat them
as a concatenation of components, one from each line over which the string is written.
For instance, in Java it is conventional to represent long strings by writing a
piece on each line and concatenating pieces with a + operator at the end of
each piece. A more difficult problem occurs when arbitrarily long lookahead may
be needed. For example, some languages like P L / I
do not treat
key- words as reserved; that is, you can use identifiers with the same
name as a keyword like DECLARE. If the lexical analyzer is presented with text
of a P L / I program that begins DECLARE ( ARG1, ARG2,... it cannot be sure
whether DECLARE is a keyword, and ARG1 and so on are variables being de-clared,
or whether DECLARE is a procedure name with its arguments. For this reason,
modern languages tend to reserve their keywords. However, if not, one can treat
a keyword like DECLARE as an ambiguous identifier, and let the parser resolve
the issue, perhaps in conjunction with symbol-table lookup.

1. Strings and Languages
An alphabet is any finite set
of symbols. Typical examples of symbols are let-ters, digits, and punctuation.
The set {0,1} is the binary alphabet.
ASCII is an important example of an alphabet; it is used in many software
systems. Uni-
switch ( *forward++ ) {
case eof:
if (forward is at end of
first buffer ) {
reload second buffer;
forward =
beginning of second buffer;
}
else if (forward is at end of second buffer ) {
reload first buffer;
forward =
beginning of first buffer;
}
else /* eof within a buffer marks the end of input */
terminate lexical
analysis;
break;
Cases for the other characters
}
Figure 3.5: Lookahead code with
sentinels
Implementing Multiway Branches
We might imagine that the switch in Fig. 3.5 requires many steps to
exe-cute, and that placing the case eof
first is not a wise choice. Actually, it doesn't matter in what order we list
the cases for each character. In prac-tice, a multiway branch depending on the
input character is be made in one step by jumping to an address found in an
array of addresses, indexed by characters.
A string over an alphabet is a finite sequence of symbols drawn from
that alphabet. In language theory, the terms "sentence" and
"word" are often used as synonyms for "string." The length
of a string s, usually written |s|, is the number of occurrences of symbols in
s. For example, banana is a string of length six. The empty string, denoted e,
is the string of length zero.
A language is any countable set of strings over some fixed alphabet.
This definition is very broad. Abstract languages like 0, the empty set, or
{e}, the set containing only the empty string, are languages under this
definition. So too are the set of all syntactically well-formed C programs and
the set of all grammatically correct English sentences, although the latter two
languages are difficult to specify exactly. Note that the definition of
"language" does not require that any meaning be ascribed to the
strings in the language. Methods for defining the "meaning" of
strings are discussed in Chapter 5.
Terms for Parts of Strings
The following string-related terms are commonly used:
A prefix of string s is any string obtained by removing
zero or more symbols from the end of s.
For example, ban, banana, and e are prefixes of banana.
A suffix of string s is any
string obtained by removing zero or more symbols from the beginning of s. For example, nana, banana, and e are
suffixes of banana.
3. A substring of s is
obtained by deleting any prefix and any suffix from s. For instance, banana, nan, and e are substrings of banana.
The proper prefixes, suffixes, and substrings of a string s are those, prefixes, suffixes, and
substrings, respectively, of s that
are not e or not equal to s itself.
5. A subsequence of s is
any string formed by deleting zero or more not necessarily
consecutive positions of s. For example, baan is a subsequence of banana.
If x and y are strings, then the
concatenation of x and y, denoted xy, is the string formed by appending y to x.
For example, if x = dog and y = house, then xy — doghouse. The empty string is
the identity under concatenation; that is, for any string s, es = se — s.
If we think of concatenation as a
product, we can define the "exponentiation" of strings as
follows. Define s° to be e, and for all
i > 0, define sl to be st~1s.
Since es = s, it follows that s1
= s. Then s2 = ss, s3 = sss, and so on.
2. Operations on Languages
In lexical analysis, the most
important operations on languages are union, con-catenation, and closure, which
are defined formally in Fig. 3.6. Union is the familiar operation on sets. The
concatenation of languages is all strings formed by taking a string from the first
language and a string from the second lan guage, in
all possible ways, and concatenating
them. The (Kleene) closure of a language L, denoted L*, is the set of strings you get by concatenating
L zero or more times. Note that L°, the
"concatenation of L zero times," is defined to be {e}, and inductively, U is Ll~1L. Finally, the positive closure, denoted L+, is the same as the Kleene
closure, but without the term L°. That is, e will not be in L+ unless it is in
L itself.
Example 3.3 i Let L be the set of
letters {A, B , . . . , Z, a, b , . . . , z} and let D be the set of digits { 0
, 1 , . . . 9} . We may think of L and D in two, essentially equivalent, ways.
One way is that L and D are, respectively, the alphabets of uppercase and
lowercase letters and of digits. The second way is that L and D are languages,
all of whose strings happen to be of length one. Here are some other languages
that can be constructed from languages L and D, using the operators of Fig.
3.6:
L U D is the set of letters and digits — strictly speaking the
language with 62 strings of length
one, each of which strings is either one letter or one digit.
LD is the set c-f 520 strings of
length two, each consisting of one letter
followed by one digit.
L4 is the set of all 4-letter strings.
4. L* is the set of all
strings of letters, including e, the empty string.
L(L U D)* is the set of all strings of letters and digits beginning with
a letter.
D+ is the set of all strings of one or more digits.
3. Regular Expressions
Suppose we wanted to describe the set of valid C identifiers. It is
almost ex-actly the language described in item (5) above; the only difference
is that the underscore is included among the letters.
In Example 3.3, we were able to describe identifiers by giving names to
sets of letters and digits and using the language operators union,
concatenation, and closure. This process is so useful that a notation called regular expressions has come into common
use for describing all the languages that can be built from these operators
applied to the symbols of some alphabet. In this notation, if letter- is established to stand for any
letter or the underscore, and digit-
is established to stand for any digit, then we could describe the language of C
identifiers by:
letter- ( letter- 1 digit )*
The vertical bar above means union, the parentheses are used to group
subex-pressions, the star means "zero or more occurrences of," and
the juxtaposition of letter, with the
remainder of the expression signifies concatenation.
The regular expressions are built recursively out of smaller regular
expres-sions, using the rules described below. Each regular expression r
denotes a language L(r), which is
also defined recursively from the languages denoted by r's subexpressions. Here
are the rules that define the regular expressions over some alphabet £ and the
languages that those expressions denote.
B A S I S: There are two rules that form the basis:
e is a regular expression, and L(e) is {e}, that is, the language whose
sole member is the empty string.
2. If a is a symbol in E, then
a is a regular expression, and L(a) = {a}, that is, the language with one string, of length one, with a in its one position. Note that by
convention, we use italics for symbols, and boldface for their corresponding
regular expression.1
I N D U C T I O N : There are four parts to the induction whereby larger regular expressions are built from smaller
ones. Suppose r and s are regular
expressions denoting languages L(r)
and L(s), respectively.
1. (r)|(s) is a regular
expression denoting the language L(r)
U L(s).
2. (r)(s) is a
regular expression denoting the language L(r)L(s).
(r)* is a regular expression
denoting (L(r))*.
(r) is a regular expression
denoting L(r). This last rule says
that we can add additional pairs of parentheses around expressions without
changing the language they denote.
As defined, regular expressions often contain unnecessary pairs of
paren-theses. We may drop certain pairs of parentheses if we adopt the
conventions that:
The unary operator * has highest
precedence and is left associative.
Concatenation has second highest
precedence and is left associative.
however, when talking about specific characters from the ASCII character
set, we shall generally use teletype font for both the character and its
regular expression.
c) | has lowest precedence and is left associative.
Under these conventions, for example, we may replace the regular
expression (a)|((b)*(c)) by a|b*c. Both expressions denote the set
of strings that are either a single a or are zero or more 6's followed by one c.
E x a m p l e 3 . 4 : Let £ = {a, 6}.
1.
The regular expression a|b denotes the language {a, b}.
2.
(a|b)(a|b) denotes {aa, ah, ba, bb}, the language of all strings of length
two over the alphabet E. Another
regular expression for the same language is aa|ab|ba|bb .
3. a* denotes the language consisting of all strings of zero or more
a's, that is, { e , a , a a , a a a , . . . } .
4. (a|b)* denotes the set of all strings consisting of zero
or more instances of a or b, that is,
all strings of a's and 6's: {e,a, b,aa,
ab, ba, bb,aaa,...}. Another regular
expression for the same language is (a*b*)*.
5. a|a*b denotes the
language {a, b, ab, aab, aaab,...}, that
is, the string a and all
strings consisting of zero or more a's
and ending in b.•
A language that can be
defined by a regular expression is called a regular set. If two regular
expressions r and s denote the same regular set, we say they are equivalent and
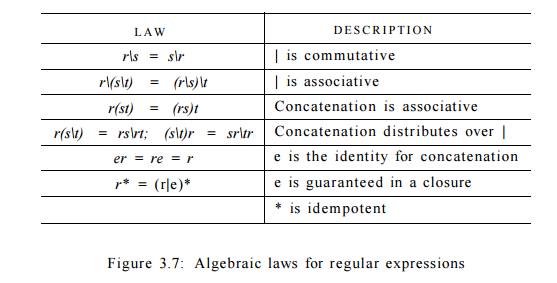
write r = s. For instance, (a|b) = (b|a). There are a number of algebraic laws
for regular expressions; each law asserts that expressions of two different
forms are equivalent. Figure 3.7 shows some of the algebraic laws that hold for arbitrary regular expressions r, s, and
t.
4. Regular Definitions
For notational convenience, we may wish to give names to certain regular
ex-pressions and use those names in subsequent expressions, as if the names
were themselves symbols. If £ is an alphabet of basic symbols, then a regular defi-nition is a sequence of
definitions of the form:

where:
Each di is a new symbol, not in E
and not the same as any other of the cTs, and
2. Each T{ is a regular expression over the alphabet E U {d1,d2,..
. ,
By restricting to E and the previously defined G T S , we avoid
recursive defini-tions, and we can construct a regular expression over E alone,
for each r$. We do so by first replacing uses of d1 in r2 (which cannot use any of the d's except for
d1), then replacing uses of d1 and d2
in r-$ by r1 and (the
substituted) r2, and so on. Finally, in
rn we replace each di, for i — 1,2, ... ,n — 1, by the substituted version of r$, each of
which has only symbols of E.
Example 3 . 5 : C identifiers are
strings of letters, digits, and underscores. Here is a regular definition for
the language of C identifiers. We shall conventionally use italics for the
symbols defined in regular definitions.
letter- -> A | B | - - - | Z | a | b | - - - | z | _
digit -> 0 j 1 j • • • j 9
id —)• letter- ( letter- 1 digit )*
Example 3 . 6 : Unsigned
numbers (integer or floating point) are strings such as 5280, 0.01234, 6.336E4,
or 1.89E-4. The regular definition
digit 0 | 1 9
digits -> digit digit*
optionalFraction - ) • . digits | e
optionalExponent ( E ( + | - | e
) digits ) | e
number -> digits optionalFraction optionalExponent
is a precise specification for this set of strings. That is, an
optionalFraction is either a decimal point (dot) followed by one or more
digits, or it is missing (the empty string). An optionalExponent, if not
missing, is the letter E followed by an optional + or - sign, followed by one
or more digits. Note that at least one digit must follow the dot, so number
does not match 1., but does match 1.0.
5. Extensions of Regular
Expressions
Since Kleene introduced regular expressions with the basic operators for
union, concatenation, and Kleene closure in the 1950s, many extensions have
been added to regular expressions to enhance their ability to specify string
patterns. Here we mention a few notational extensions that were first
incorporated into Unix utilities such as Lex that are particularly useful in
the specification lexical analyzers. The references to this chapter contain a
discussion of some regular-expression variants in use today.
1. One or more instances. The unary, postfix operator + represents the
positive closure of a regular expression and its language. That is, if r is
a regular expression, then ( r ) +
denotes the language (L(r)) + . The operator
+ has the same precedence and associativity as the operator *. Two
useful algebraic laws, r* = r+1e and r+ = rr* = r*r relate the Kleene closure
and positive closure.
2. Zero or one instance. The unary postfix operator ? means "zero
or one occurrence." That is, r? is equivalent to r|e, or put another way,
L(r?) = L(r) U {e}. The ? operator has the same precedence and associativity
as and + .
3. Character classes. A regular expression aifal • • • 1an, where the
a^s are each symbols of the alphabet, can be replaced by the shorthand [aia,2 •
• - an]. More importantly, when 0 1 , 0 2 , . . . , a n f ° r m a logical
sequence, e.g., consecutive uppercase letters, lowercase letters, or digits,
we can replace them by o i - a n , that
is, just the first and last separated by a hyphen. Thus, [abc] is shorthand for
a|b|c, and [a-z] is shorthand for
a|b| . -- |z .
Example 3 . 7: of Example 3.5
Using these shorthands, we can rewrite the regular definition as:
letter. -> [A-Za-z_]
digit -> [0-9]
id -> letter- ( letter 1 digit )*
The regular definition of Example 3.6 can also be simplified:
digit -> [0-9]
digits —>• digit+
number -»• digits (. digits)? ( E [+-]? digits )? •
6. Exercises for Section 3.3
E x e r c i se 3 . 3 . 1 : Consult the language reference manuals to determine (i) the sets of characters that form the input alphabet (excluding those
that may only appear in character strings or comments), (ii) the lexical form of numerical constants, and (Hi) the lexical form of identifiers,
for each of the following languages: (a) C (b) C + + (c) C# (d) Fortran (e)
Java (f) Lisp (g) SQL.
! Exercise 3 . 3 . 2 : Describe the languages denoted
by the following regular ex-
pressions:
a(a|b)*a.
((e|a)b*)*.
(a|b)*a(a|b)(a|b).
a*ba*ba*ba*.
e) (aa|bb)*((ab|ba)(aa|bb)*(ab|ba)(aa|bb)*)*.
Exercise 3 . 3 . 3 : In a string of length n, how
many of the following are there?
Prefixes.
Suffixes.
Proper prefixes.
d) Substrings.
e) Subsequences.
Exercise 3 . 3 . 4 : Most languages are case sensitive, so keywords can be written only
one way, and the regular expressions describing their lexeme is very simple.
However, some languages, like SQL, are case
insensitive, so a keyword can be written either in lowercase or in
uppercase, or in any mixture of cases. Thus, the SQL keyword SELECT can also be written s e l e c t , S e l e c t , or sElEcT, for instance. Show how to write
a regular expression for a keyword in a case-insensitive language. Illustrate
the idea by writing the expression for "select" in SQL.
Exercise 3 . 3 . 5: Write regular definitions for the following languages:
All strings of lowercase letters
that contain the five vowels in order.
All strings of lowercase letters
in which the letters are in ascending lexi-cographic order.
Comments, consisting of a string surrounded by /* and */, without an
intervening */, unless it is inside double-quotes (").
!! d) All strings of digits with no repeated digits. Hint: Try this
problem first with a few digits, such as {0,1,2} .
!! e) All strings of digits with at most one repeated digit.
!! f) All strings of a's and 6's with an even number of a's and an odd
number of 6's.
g) The set of Chess moves, in the
informal notation, such as p - k4 or kbpxqn .
!! h) All strings of a's and 6's that do not contain the substring a66.
i) All strings of a's and 6's
that do not contain the subsequence a66.
Exercise 3 . 3 . 6: Write character classes for the following sets of
characters:
a) The first ten letters (up
to "j") in either upper or
lower case.
The lowercase consonants.
The "digits" in a
hexadecimal number (choose either upper or lower case for the
"digits" above 9 ) .
The characters that can appear at
the end of a legitimate English sentence (e.g., exclamation point).
The following exercises, up to and including Exercise 3.3.10, discuss
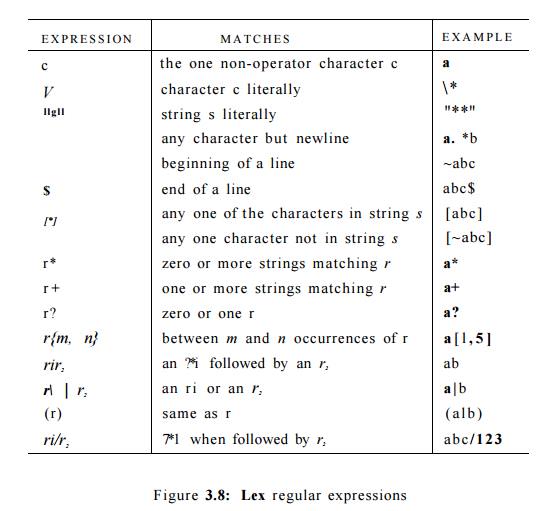
the extended regular-expression notation from Lex (the lexical-analyzer
generator that we shall discuss extensively in Section 3.5). The extended
notation is listed in Fig. 3.8.
Exercise 3.3. 7: Note that these regular expressions give all of the
following symbols (operator characters) a special meaning:
1 » . ~ $ [ ] * + ? { } I /
Their special meaning must be turned off if they are needed to represent
them-selves in a character string. We can do so by quoting the character within
a string of length one or more; e.g., the regular expression "**"
matches the string **. We can also get the literal meaning of an operator
character by preceding it by a backslash. Thus, the regular expression 1 * 1 *
also matches the string
**. Write a regular expression
that matches the string "1 .
Exercise 3.3.8: In Lex, a
complemented character class represents any character except the
ones listed in the character class. We
denote a complemented class by using " as the first character; this symbol
(caret) is not itself part of the class being complemented, unless it is listed
within the class itself. Thus,
[~A-Za-z] matches any character that is not an uppercase or lowercase
letter, and [~\~] represents any character but the caret (or newline, since
newline cannot be in any character class). Show that for every regular
expression with complemented character classes, there is an equivalent regular
expression with-out complemented character classes.
! Exercise 3.3.9 : The regular expression r{m, n] matches from m to n
occur-rences of the pattern r. For example, a [1,5] matches a string of one to
five a's. Show that for every regular expression containing repetition
operators of this form, there is an equivalent regular expression without
repetition operators.
! Exercise 3.3.10 : The operator " matches the left end of a line,
and $ matches the right end of a line.
The operator " is also used to introduce complemented character
classes, but the context always makes it clear which meaning is intended. For
example, ~[~aeiou]* $ matches any complete line that does not contain a
lowercase vowel.
How do you tell which meaning of
A is intended?
Can you always replace a regular
expression using the " and $ operators by an equivalent expression that
does not use either of these operators?
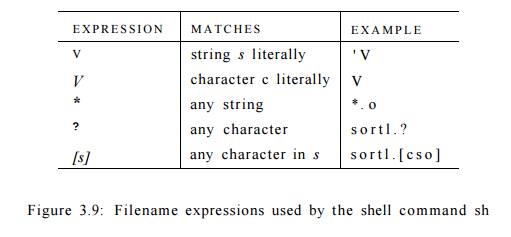
! Exercise 3.3.11 : The UNIX shell command sh uses the operators in Fig.
3.9 in filename expressions to describe sets of file names. For example, the
filename expression * . o matches all file names ending in .o; s o r t l . ? matches all file-names of
the form s o r t . c, where c is any character.
Show how sh filename
expressions can be replaced by equivalent regular expressions using only
the basic union, concatenation, and closure operators.
! Exercise 3 . 3 . 1 2 : SQL allows a rudimentary form of patterns in which two characters have special meaning:
underscore (_) stands for any one character and percent-sign (%) stands for any
string of 0 or more characters. In addition, the programmer may define any
character, say e, to be the escape character, so e preceding an e preceding _,
% or another e gives the character that follows its literal meaning. Show how
to express any SQL pattern as a regular expression, given that we know which
character is the escape character.
Related Topics