Multipliers

Multipliers

Multiplication of binary numbers is usually implemented in microprocessors and microcomputers by using repeated addition and shift operations. Since the binary adders are designed to add only two binary numbers at a time, instead of adding all the partial products at the end, they are added two at a time and their sum is accumulated in a register called the accumulator register. Also, when the multiplier bit is ‘0‘, that very partial product is ignored, as an all ‘0‘ line does not affect the final result. The basic hardware arrangement of such a binary multiplier would comprise shift registers for the multiplicand and multiplier bits, an accumulator register for storing partial products, a binary parallel adder and a clock pulse generator to time various operations.

Binary multipliers are also available in IC form. Some of the popular type numbers in the TTL family include 74261 which is a 2 × 4 bit multiplier (a four-bit multiplicand designated as B0,B1,B2,B3 and B4, and a two-bit multiplier designated as M0, M1 and M2.

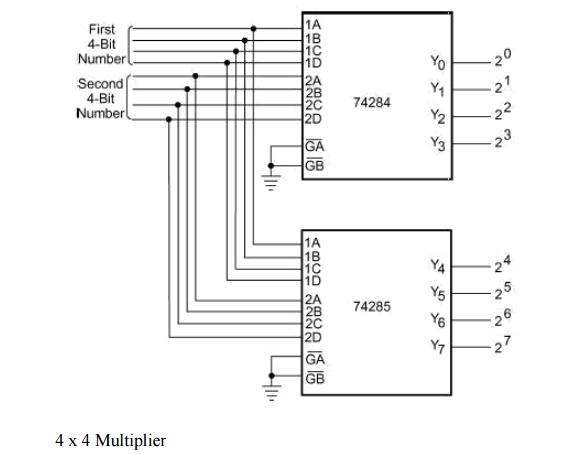
The MSBs B4 and M2 are used to represent signs. 74284 and 74285 are 4 × 4 bit multipliers. They can be used together to perform high-speed multiplication of two four-bit numbers. Figure 3.14 shows the arrangement. The result of multiplication is often required to be stored in a register. The size of this register (accumulator) depends upon the number of bits in the result, which at the most can be equal to the sum of the number of bits in the multiplier and multiplicand. Some multipliers ICs have an in-built register.

Many microprocessors do not have in their ALU the hardware that can perform multiplication or other complex arithmetic operations such as division, determining the square root, trigonometric functions, etc. These operations in these microprocessors are executed through software. For example, a multiplication operation may be accomplished by using a software program that does multiplication through repeated execution of addition and shift instructions. Other complex operations mentioned above can also be executed with similar programs. Although the use of software reduces the hardware needed in the microprocessor, the computation time in general is higher in the case of software-executed operations when compared with the use of hardware to perform those operations.

Design Using MSI devices

When designing logic circuits, the "discrete logic gates"; i.e., individual AND, OR, NOT etc. gates, are often neither the simplest nor the most economical devices we could use. There are many standard MSI(medium scale integrated) and LSI(Large scle integrated) circuits, or functions available, which can do many of the things commonly required in logic circuits. Often these MSI and LSI circuits do not fit our requirements exactly, and it is often necessary to use discrete logic to adapt these circuits for our application.

However, the number and type o these LSI and VLSI (very large scale integrated) circuits is steadily increasing, and it is difficult to always be aware of the best possible circuits available for a given problem. Also, systematic design methods are difficult to devise when the types of logic device available keeps increasing. In general the "best" design procedure is to attempt to find a LSI device which can perform the required function, or which can be modified using other devices to perform the required function. If nothing is available, then the function should be implemented with several MSI devices. Only as a last option should the entire function be implemented with discrete logic gates. In fact, with present technology, it is becoming increasingly cost-effective to implement a design as one or more dedicated VLSI devices.

When designing all but the simplest logic devices, a "top-down" approch should be adopted. The device should be specified in block form, and attempt to implement each block with a small number of LSI or MSI functions. Each block which cannot be implemented directly can be then broken into smaller blocks, and process repeated, until each block is fully implemented.

Of course, a good knowledge of what LSI and MSI functions are available in the appropriate technology makes this process simpler.