Half Subtractor

Half-Subtractor

We will study the use of adder circuits for subtraction operations in the following pages. Before we do that, we will briefly look at the counterparts of half-adder and full adder circuits in the half-subtractor and full subtractor for direct implementation of subtraction operations using logic gates.

A half-subtractor is a combinational circuit that can be used to subtract one binary digit from another to produce a DIFFERENCE output and a BORROW output. The BORROW output here specifies whether a ‘1‘ has been borrowed to perform the subtraction. The truth table of a half-subtractor, as shown in Fig. 3.9, explains this further. The Boolean expressions for the two outputs are given by the equations

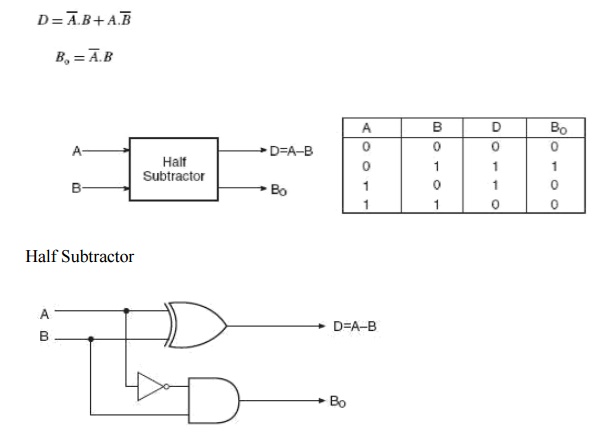
Logic Diagram of a Half Subtractor

It is obvious that there is no further scope for any simplification of the Boolean expressions given by above equations. While the expression for the DIFFERENCE (D) output is that of an EX-OR gate, the expression for the BORROW output (Bo) is that of an AND gate with input A complemented before it is fed to the gate. Figure 3.10 shows the logic implementation of a half-subtractor. Comparing a half-subtractor with a half-adder, we find that the expressions for the SUM and DIFFERENCE outputs are just the same. The expression for BORROW in the case of the half-subtractor is also similar to what we have for CARRY in the case of the half-adder. If the input A, that is, the minuend, is complemented, an AND gate can be used to implement the BORROW output. Note the similarities between the logic diagrams of Fig. 3.3 (half-adder) and Fig. 3.10 (half-subtractor).