Chapter: Digital Logic Circuits : Combinational Circuits
Logic Implementation and circuit diagram of Half and Full Adder
Binary Adder
Half-Adder
A half-adder is an arithmetic circuit block that can be used to add two bits. Such a circuit thus has two inputs that represent the two bits to be added and two outputs, with one producing the SUM output and the other producing the CARRY. Figure 3.2 shows the truth table of a half-adder, showing all possible input combinations and the corresponding outputs.
The Boolean expressions for the SUM and CARRY outputs are given by the equations below
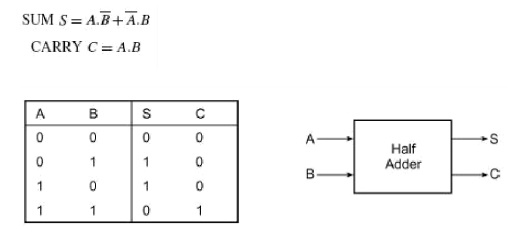
Truth Table of Half Adder
An examination of the two expressions tells that there is no scope for further simplification. While the first one representing the SUM output is that of an EX-OR gate, the second one representing the CARRY output is that of an AND gate. However, these two expressions can certainly be represented in different forms using various laws and theorems of Boolean algebra to illustrate the flexibility that the designer has in hardware-implementing as simple a combinational function as that of a half-adder.
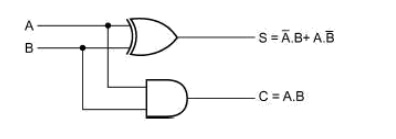
Logic Implementation of Half Adder
Although the simplest way to hardware-implement a half-adder would be to use a two-input EX-OR gate for the SUM output and a two-input AND gate for the CARRY output, as shown in Fig. 3.3, it could also be implemented by using an appropriate arrangement of either NAND or NOR gates.
Full Adder
A full adder circuit is an arithmetic circuit block that can be used to add three bits to produce a SUM and a CARRY output. Such a building block becomes a necessity when it comes to adding binary numbers with a large number of bits. The full adder circuit overcomes the limitation of the half-adder, which can be used to add two bits only. Let us recall the procedure for adding larger binary numbers. We begin with the addition of LSBs of the two numbers. We record the sum under the LSB column and take the carry, if any, forward to the next higher column bits. As a result, when we add the next adjacent higher column bits, we would be required to add three bits if there were a carry from the previous addition. We have a similar situation for the other higher column bits. Also until we reach the MSB. A full adder is therefore essential for the hardware implementation of an adder circuit capable of adding larger binary numbers. A half-adder can be used for addition of LSBs only.
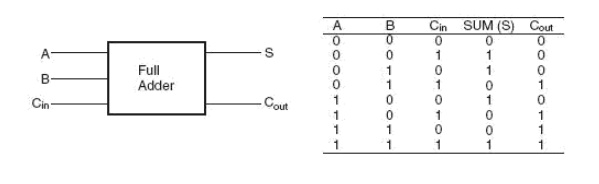
Truth Table of Full Adder
Figure shows the truth table of a full adder circuit showing all possible input combinations and corresponding outputs. In order to arrive at the logic circuit for hardware implementation of a full adder, we will firstly write the Boolean expressions for the two output variables, that is, the SUM and CARRY outputs, in terms of input variables. These expressions are then simplified by using any of the simplification techniques described in the previous chapter. The Boolean expressions for the two output variables are given in Equation below for the SUM output (S) and in above Equation for the CARRY output (Cout):
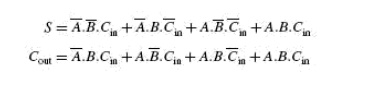
The next step is to simplify the two expressions. We will do so with the help of the Karnaugh mapping technique. Karnaugh maps for the two expressions are given in Fig. 3.5(a) for the SUM output and Fig. 3.5(b) for the CARRY output. As is clear from the two maps, the expression for the SUM (S) output cannot be simplified any further, whereas the simplified Boolean expression for Cout is given by the equation
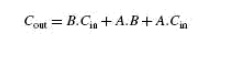
Figure shows the logic circuit diagram of the full adder. A full adder can also be seen to comprise two half-adders and an OR gate. The expressions for SUM and CARRY outputs can be rewritten as follows:
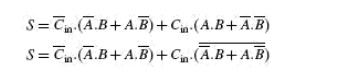
Similarly, the expression for CARRY output can be rewritten as follows:
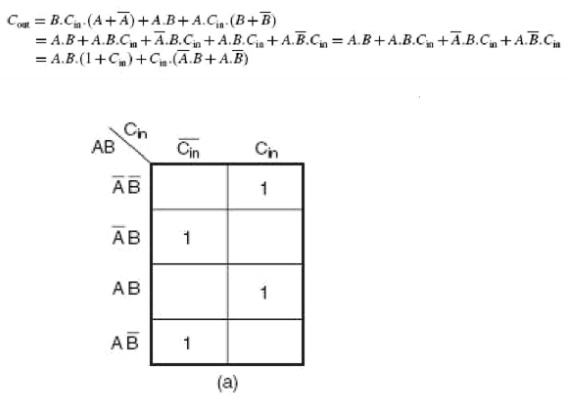
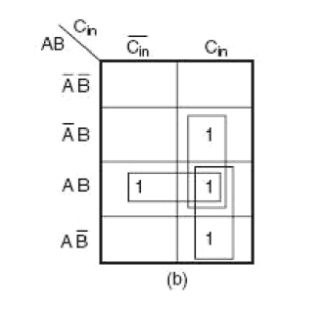
Karnaugh Map for the sum and carry out of a full adder
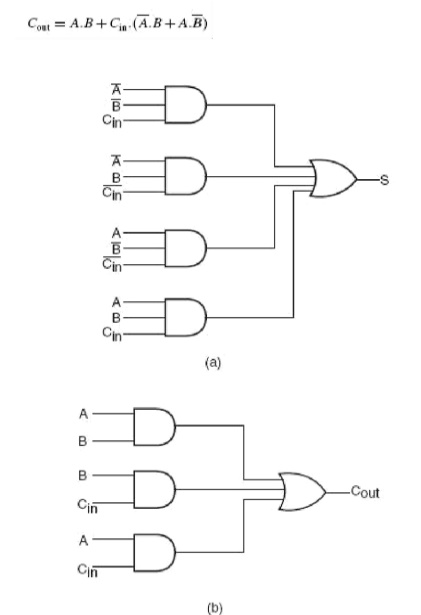
Logic circuit diagram of full adder
Boolean expression above can be implemented with a two-input EX-OR gate provided that one of the inputs is Cin and the other input is the output of another two-input EX-OR gate with A and B as its inputs. Similarly, Boolean expression above can be implemented by ORing two minterms. One of them is the AND output of A and B. The other is also the output of an AND gate whose inputs are Cin and the output of an EX-OR operation on A and B. The whole idea of writing the Boolean expressions in this modified form was to demonstrate the use of a half-adder circuit in building a full adder. Figure 3.7(a) shows logic implementation of Equations above. Figure 3.7(b) is nothing but Fig. 3.7(a) redrawn with the portion of the circuit representing a half-adder replaced with a block. The full adder of the type described above forms the basic building block of binary adders. However, a single full adder circuit can be used to add one-bit binary numbers only. A cascade arrangement of these adders can be used to construct adders capable of adding binary numbers with a larger number of bits. For example, a four-bit binary adder would require four full adders of the type shown in Fig. 3.7 to be connected in cascade. Figure 3.8 shows such an arrangement. (A3A2A1A0) and (B3B2B1B0) are the two binary numbers to be added, with A0 and B0 representing LSBs and A3 and B3 representing MSBs of the two numbers.
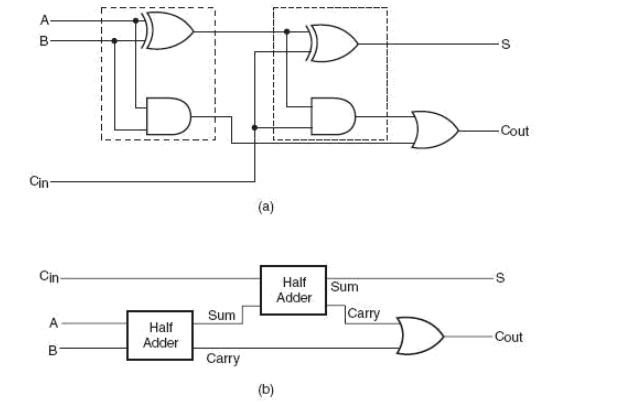
Logic Implementation of a full adder with Half Adders
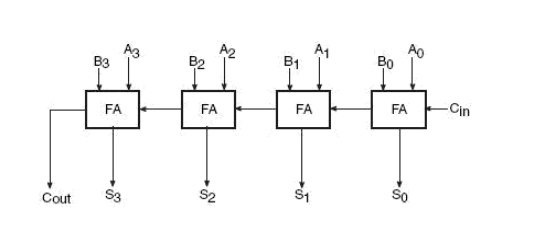
Four Bit Binary Adder
Related Topics