Chapter: Digital Logic Circuits : Combinational Circuits
Different Styles of row and column identification - K map
Different Styles of row and column identification
Having accounted for groups with all 1s, the minimum ‘sum-of-products‘ or ‘product-of-sums‘ expressions can be written directly from the Karnaugh map. Minterm Karnaugh map and Maxterm Karnaugh map of the Boolean function of a two-input OR gate. The Minterm and Maxterm Boolean expressions for the two-input OR gate are as follows:
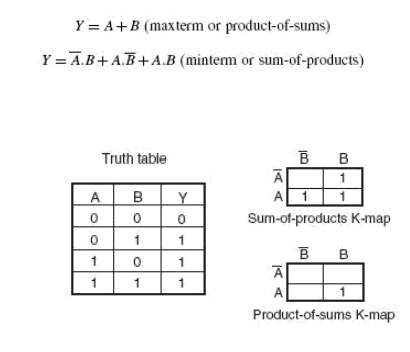
Minterm Karnaugh map and Maxterm Karnaugh map of the three variable Boolean function
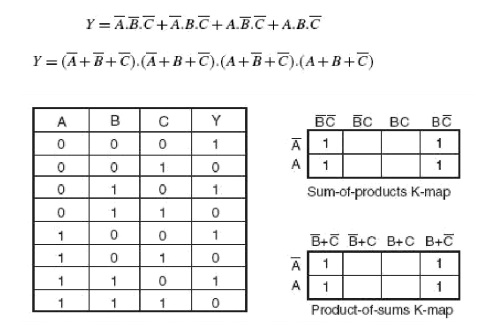
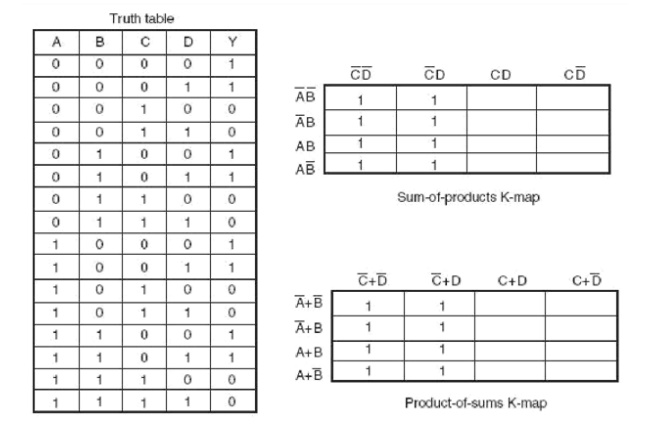
The truth table, Minterm Karnaugh map and Maxterm Karnaugh map of the four variable
Boolean function
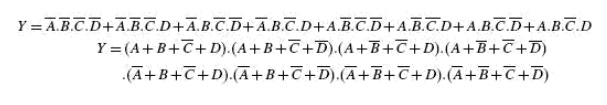
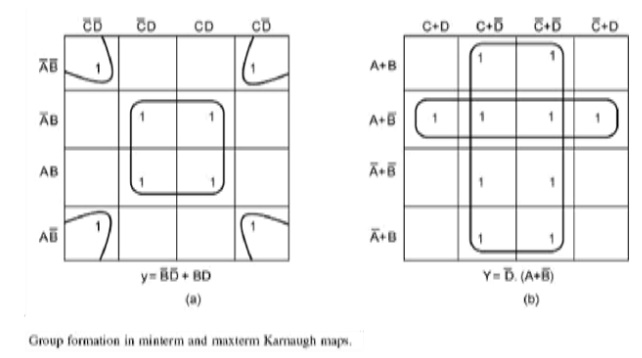
To illustrate the process of forming groups and then writing the corresponding minimized Boolean expression, The below figures respectively show minterm and maxterm Karnaugh maps for the Boolean functions expressed by the below equations. The minimized expressions as deduced from Karnaugh maps in the two cases are given by Equation in the case of the minterm Karnaugh map and Equation in the case of the maxterm Karnaugh map:
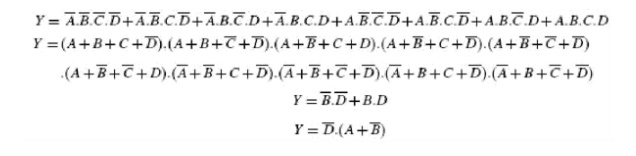
Quine–McCluskey Tabular Method
The Quine–McCluskey tabular method of simplification is based on the complementation theorem, which says that
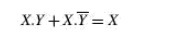
where X represents either a variable or a term or an expression and Y is a variable. This theorem implies that, if a Boolean expression contains two terms that differ only in one variable, then they can be combined together and replaced with a term that is smaller by one literal. The same procedure is applied for the other pairs of terms wherever such a reduction is possible. All these terms reduced by one literal are further examined to see if they can be reduced further. The process continues until the terms become irreducible. The irreducible terms are called prime implicants. An optimum set of prime implicants that can account for all the original terms then constitutes the minimized expression. The technique can be applied equally well for minimizing sum-of-products and product of- sums expressions and is particularly useful for Boolean functions having more than six variables as it can be mechanized and run on a computer. On the other hand, the Karnaugh mapping method, to be discussed later, is a graphical method and becomes very cumbersome when the number of variables exceeds six. The step-by-step procedure for application of the tabular method for minimizing Boolean expressions,both sum-of-products and product-of-sums, is outlined as follows:
1. The Boolean expression to be simplified is expanded if it is not in expanded form.
2. Different terms in the expression are divided into groups depending upon the number of 1s they have.
True and complemented variables in a sum-of-products expression mean ‘1‘ and ‘0‘ respectively.The reverse is true in the case of a product-of-sums expression. The groups are then arranged, beginning with the group having the least number of 1s in its included terms. Terms within the same group are arranged in ascending order of the decimal numbers represented by these terms. As an illustration, consider the expression
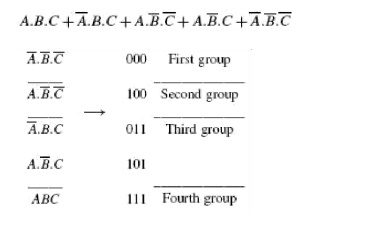
As another illustration, consider a product-of-sums expression given by
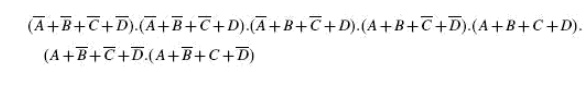
The formation of groups and the arrangement of terms within different groups for the product-of sums expression are as follows:
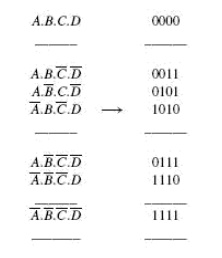
It may be mentioned here that the Boolean expressions that we have considered above did not contain any optional terms. If there are any, they are also considered while forming groups. This completes the first table.
3. The terms of the first group are successively matched with those in the next adjacent higher order group to look for any possible matching and consequent reduction. The terms are considered matched when all literals except for one match. The pairs of matched terms are replaced with a single term where the position of the unmatched literals is replaced with a dash (—). These new terms formed as a result of the matching process find a place in the second table. The terms in the first table ∗that do not find a match are called the prime implicants and are marked with an asterisk ( ). The matched terms are ticked (_).
4. Terms in the second group are compared with those in the third group to look for a possible match.Again, terms in the second group that do not find a match become the prime implicants.
5. The process continues until we reach the last group. This completes the first round of matching.The terms resulting from the matching in the first round are recorded in the second table.
6. The next step is to perform matching operations in the second table. While comparing the terms for a match, it is important that a dash (—) is also treated like any other literal, that is, the dash signs also need to match. The process continues on to the third table, the fourth table and so on until the terms become irreducible any further.
7. An optimum selection of prime implicants to account for all the original terms constitutes the terms for the minimized expression. Although optional (also called ‘don‘t care‘) terms are considered for matching, they do not have to be accounted for once prime implicants have been identified.
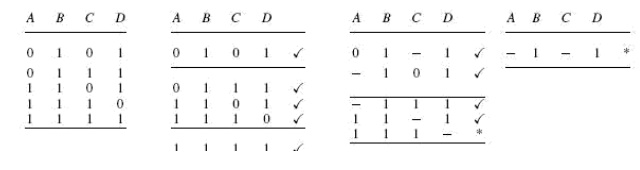
Let us consider an example. Consider the following sum-of-products expression:

The second round of matching begins with the table shown on the previous page. Each term in the first group is compared with every term in the second group. For instance, the first term in the first group 00−1 matches with the second term in the second group 01−1 to yield 0−−1, which is recorded in the table shown below. The process continues until all terms have been compared for a possible match. Since this new table has only one group, the terms contained therein are all prime implicants. In the present example, the terms in the first and second tables have all found a match. But that is not always the case.
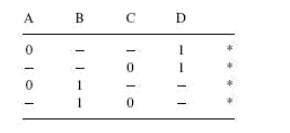
The next table is what is known as the prime implicant table. The prime implicant table contains all the original terms in different columns and all the prime implicants recorded in different rows as shown below:
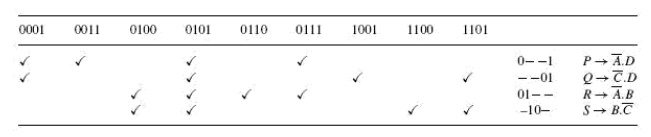
Each prime implicant is identified by a letter. Each prime implicant is then examined one by one and the terms it can account for are ticked as shown. The next step is to write a product-of-sums expression using the prime implicants to account for all the terms. In the present illustration, it is given as follows.
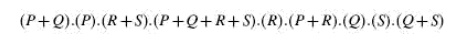
Obvious simplification reduces this expression to PQRS which can be interpreted to mean that all prime implicants, that is, P, Q, R and S, are needed to account for all the original terms. Therefore, the minimized expression =
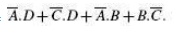
What has been described above is the formal method of determining the optimum set of prime implicants. In most of the cases where the prime implicant table is not too complex, the exercise can be done even intuitively. The exercise begins with identification of those terms that can be accounted for by only a single prime implicant. In the present example, 0011, 0110, 1001 and 1100 are such terms. As a result, P, Q, R and S become the essential prime implicants. The next step is to find out if any terms have not been covered by the essential prime implicants. In the present case, all terms have been covered by essential prime implicants. In fact, all prime implicants are essential prime implicants in the present example. As another illustration, let us consider a product-of-sums expression given by
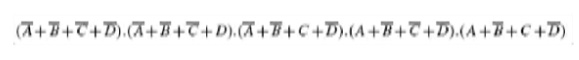
The procedure is similar to that described for the case of simplification of sum-of-products expressions.
The resulting tables leading to identification of prime implicants are as follows:
The prime implicant table is constructed after all prime implicants have been identified to look for the optimum set of prime implicants needed to account for all the original terms. The prime implicant table shows that both the prime implicants are the essential ones:

Universal Gates
OR, AND and NOT gates are the three basic logic gates as they together can be used to construct the logic circuit for any given Boolean expression. NOR and NAND gates have the property that they individually can be used to hardware-implement a logic circuit corresponding to any given Boolean expression. That is, it is possible to use either only NAND gates or only NOR gates to implement any Boolean expression. This is so because a combination of NAND gates or a combination of NOR gates can be used to perform functions of any of the basic logic gates. It is for this reason that NAND and NOR gates are universal gates. As an illustration, Fig. 4.24 shows how two-input NAND gates can be used to construct a NOT circuit, a two-input AND gate and a two-input OR gate. Figure shows the same using NOR gates. Understanding the conversion of NAND to OR and NOR to AND requires the use of DeMorgan‘s theorem, which is discussed in Chapter 6 on Boolean algebra.
These are gates where we need to connect an external resistor, called the pull-up resistor, between the output and the DC power supply to make the logic gate perform the intended logic function. Depending on the logic family used to construct the logic gate, they are referred to as gates with open collector output (in the case of the TTL logic family) or open drain output (in the case of the MOS logic family).
5. The advantage of using open collector/open drain gates lies in their capability of providing an ANDing operation when outputs of several gates are tied together through a common pull-up resistor,
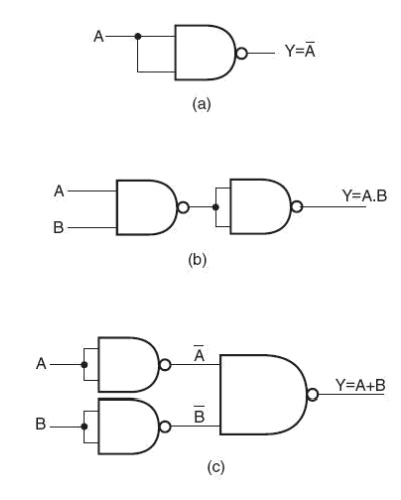
Implementation of basic logic gates using only NAND gates.
without having to use an AND gate for the purpose. This connection is also referred to as WIRE-AND connection. Figure shows such a connection for open collector NAND gates. The output in this case would be
WIRE-AND connection with open collector/drain devices.
The disadvantage is that they are relatively slower and noisier. Open collector/drain devices are therefore not recommended for applications where speed is an important consideration.
The Exclusive-OR function
One element conspicuously missing from the set of Boolean operations is that of Exclusive-OR. Whereas the OR function is equivalent to Boolean addition, the AND function to Boolean multiplication, and the NOT function (inverter) to Boolean complementation, there is no direct Boolean equivalent for Exclusive-OR. This hasn‘t stopped people from developing a symbol to represent it, though:
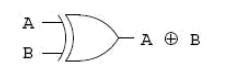
This symbol is seldom used in Boolean expressions because the identities, laws, and rules of simplification involving addition, multiplication, and complementation do not apply to it. However, there is a way to represent the Exclusive-OR function in terms of OR and AND, as has been shown in previous chapters: AB‘ + A‘B.
Related Topics