Miscellaneous Problems

Miscellaneous Problems

1. The probability function of a random variable X is given by

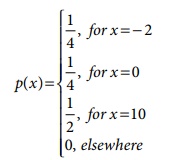
Evaluate the following probabilities.

(i) P ( X ≤ 0) , (ii) P ( X < 0) , (iii) P ( |X| ≤ 2) and (iv) P ( 0 ≤ X ≤10)

2. Let X be a random variable with cumulative distribution function

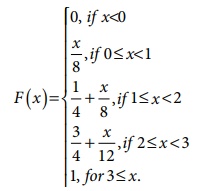
(a) Compute: (i) P (1 ≤ X≤ 2) and (ii) P (X = 3) .

(b) Is X a discrete random variable? Justify your answer.

3. The p.d.f. of X is defined as

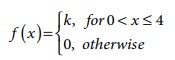
Find the value of k and also find P ( 2 ≤ X ≤ 4) .

4. The probability distribution function of a discrete random variable X is

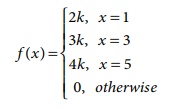
where k is some constant. Find (a) k and (b) P (X > 2) .

5. The probability density function of a continuous random variable X is

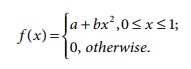
where a and b are some constants. Find (i) a and b if E ( X) = 3/5 (ii) Var ( X) .

6. Prove that if E ( X) = 0, then V ( X ) = E ( X² ) .

7. What is the expected value of a game that works as follows: I flip a coin and, if tails pay you ₹ 2; if heads pay you ₹ 1. In either case I also pay you ₹ 50.

8. Prove that, (i) V (aX ) = a2V ( X ) , and (ii) V ( X + b) = V ( X )

9. Consider a random variable X with p.d.f

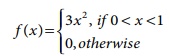
Find E ( X) and V(3X–2).

10. The time to failure in thousands of hours of an important piece of electronic equipment used in a manufactured DVD player has the density function

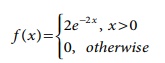
Find the expected life of this piece of equipment.

Answers:

1. (i) ½ (ii) ¼ (iii) ½ (iv) ¾ 

2. (a) (i) 13/24 (ii) 0 (b) X is NOT discrete since F is not a step function.

3. 1/4:1/2 

4. (a) 1/9 (b) 7/9 

5. (i) 3/5,6/5 (ii) 2/25 

7. 2

9. 3/4, 27/80

10. 1/2