Exercise 6.1: Random variable

Exercise 6.1

1. Construct cumulative distribution function for the given probability distribution.

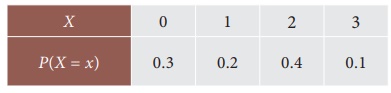
2. Let X be a discrete random variable with the following p.m.f

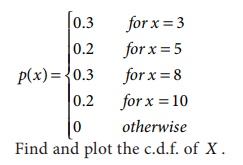
Find and plot the c.d.f. of X .

3. The discrete random variable X has the following probability function

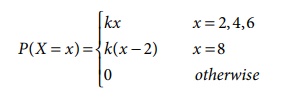
where k is a constant. Show that k = 1/81

4. The discrete random variable X has the probability function

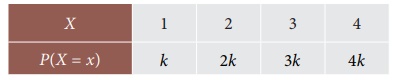
Show that k = 0 ⋅ 1 .

5. Two coins are tossed simultaneously. Getting a head is termed as success. Find the probability distribution of the number of successes.

6. A continuous random variable X has the following probability function

(i) Find k

(ii) Ealuate p( x < 6), p(x ≥ 6) and p(0 < x < 5)

(iii) If P(X ≤ x) > 1/2 , then find the minimum value of x .

7. The distribution of a continuous random variable X in range (–3, 3) is given by p.d.f.

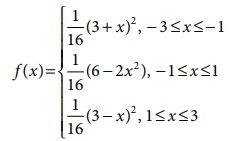
Verify that the area under the curve is unity.

8. A continuous random variable X has the following distribution function:

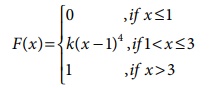
Find (i) k and (ii) the probability density function.

9. The length of time (in minutes) that a certain person speaks on the telephone is found to be random phenomenon, with a probability function specified by the probability density function f (x) as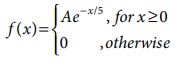 

(a) Find the value of A that makes f (x) a p.d.f.

(b) What is the probability that the number of minutes that person will talk over the phone is (i) more than 10 minutes, (ii) less than 5 minutes and (iii) between 5 and 10 minutes.

10. Suppose that the time in minutes that a person has to wait at a certain station for a train is found to be a random phenomenon with a probability function specified by the distribution function

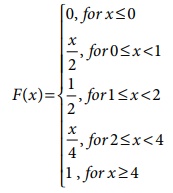
(a) Is the distribution function continuous? If so, give its probability density function?

(b) What is the probability that a person will have to wait (i) more than 3 minutes, (ii) less than 3 minutes and (iii) between 1 and 3 minutes?

11. Define random variable.

12. Explain what are the types of random variable?

13. Define discrete random variable.

14. What do you understand by continuous random variable?

15. Describe what is meant by a random variable.

16. Distinguish between discrete and continuous random variable.

17. Explain the distribution function of a random variable.

18. Explain the terms (i) probability mass function, (ii) probability density function and (iii) probability distribution function.

19. What are the properties of (i) discrete random variable and (ii) continuous random variable?

20. State the properties of distribution function.

Answers: