Random Variable and Mathematical Expectation - Choose the correct Answer | 12th Business Maths and Statistics : Chapter 6 : Random Variable and Mathematical Expectation
Chapter: 12th Business Maths and Statistics : Chapter 6 : Random Variable and Mathematical Expectation
Choose the correct Answer
Choose the correct Answer
1. Value which is obtained by multiplying possible values of random variable with probability of occurrence and is equal to weighted average is called
(a) Discrete value
(b) Weighted value
(c) Expected value
(d) Cumulative value
2. Demand of products per day for three days are 21, 19, 22 units and their respective probabilities are 0 29, 0 40, 0 35. Pofit per unit is 0 50 paisa then expected profits for three days are
(a) 21, 19, 22
(b) 21.5, 19.5, 22.5
(c) 0.29, 0.40, 0.35
(d) 3.045, 3.8, 3.85
3. Probability which explains x is equal to or less than particular value is classified as
(a) discrete probability
(b) cumulative probability
(c) marginal probability
(d) continuous probability
4. Given E(X) = 5 and E(Y) = -2, then E(X – Y) is
(a) 3
(b) 5
(c) 7
(d) –2
5. A variable that can assume any possible value between two points is called
(a) discrete random variable
(b) continuous random variable
(c) discrete sample space
(d) random variable
6. A formula or equation used to represent the probability distribution of a continuous random variable is called
(a) probability distribution
(b) distribution function
(c) probability density function
(d) mathematical expectation
7. If X is a discrete random variable and p(x) is the probability of X , then the expected value of this random variable is equal to
(a) ∑ f ( x)
(b) ∑ [x + f ( x)]
(c) ∑ f ( x) + x
(d) ∑ xp( x)
8. Which of the following is not possible in probability distribution?
(a) ∑ p( x)≥ 0
(b) ∑ p( x) = 1
(c) ∑ x p( x) = 2
(d) p(x) = − 0.5
9. If c is a constant, then E (c) is
(a) 0
(b) 1
(c) c f
(d) c
10. A discrete probability distribution may be represented by
(a) table
(b) graph
(c) mathematical equation
(d) all of these
11. A probability density function may be represented by:
(a) table
(b) graph
(c) mathematical equation
(d) both (b) and (c)
12. If c is a constant in a continuous probability distribution, then p(x = c) is always equal to
(a) zero
(b) one
(c) negative
(d) does not exist
13. E [X − E ( X)] is equal to
(a) E (X)
(b) V (X)
(c) 0
(d) E (X) − X
14. E [X − E ( X)]2 is
(a) E ( X)
(b) E ( X2)
(c) V ( X)
(d) S. D(X)
15. If the random variable takes negative values, then the negative values will have
(a) positive probabilities
(b) negative probabilities
(c) constant probabilities
(d) difficult to tell
16. If we have f ( x) = 2 x , 0 ≤ x ≤1 , then f ( x) is a
(a) probability distribution
(b) probability density function
(c) distribution function
(d) continuous random variable
17. 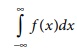 is always equal to
is always equal to
(a) zero
(b) one
(c) E ( X)
(d) f ( x) +1
18. A listing of all the outcomes of an experiment and the probability associated with each outcome is called
(a) probability distribution
(b) probability density function
(c) attributes
(d) distribution function
19. Which one is not an example of random experiment?
(a) A coin is tossed and the outcome is either a head or a tail
(b) A six-sided die is rolled
(c) Some number of persons will be admitted to a hospital emergency room during any hour.
(d) All medical insurance claims received by a company in a given year.
20. A set of numerical values assigned to a sample space is called
(a) random sample
(b) random variable
(c) random numbers
(d) random experiment
21. A variable which can assume finite or countably infinite number of values is known as
(a) continuous
(b) discrete
(c) qualitative
(d) none of them
22. The probability function of a random variable is defined as
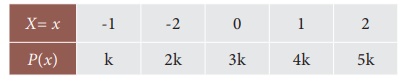
Then k is equal to
(a) zero
(b) 1/4
(c) 1/15
(d) one
23. If p( x) = 1/10 , x = 10, then E ( X) is
(a) zero
(b) 6/8
(c) 1
(d) –1
24. A discrete probability function p( x) is always
(a) non-negative
(b) negative
(c) one
(d) zero
25. In a discrete probability distribution the sum of all the probabilities is always equal to
(a) zero
(b) one
(c) minimum
(d) maximum
26. An expected value of a random variable is equal to it’s
(a) variance
(b) standard deviation
(c) mean
(d) covariance
27. A discrete probability function p(x) is always non-negative and always lies between
(a) 0 and ∞
(b) 0 and 1
(c) –1 and +1
(d) –∞ and +∞
28. The probability density function p(x) cannot exceed
(a) zero
(b) one
(c) mean
(d) infinity
29. The height of persons in a country is a random variable of the type
(a) discrete random variable
(b) continuous random variable
(c) both (a) and (b)
(d) neither (a) nor (b)
30. The distribution function F(x) is equal to
(a) P ( X = x)
(b) P ( X ≤ x) (c)
(c) P ( X ≥ x)
(d) all of these
Related Topics