Discrete random variable

Discrete random variable

Definition 6.2

A variable which can assume finite number of possible values or an infinite sequence of countable real numbers is called a discrete random variable.

Examples of discrete random variable:

·        Marks obtained in a test.

·        Number of red marbles in a jar.

·        Number of telephone calls at a particular time.

·        Number of cars sold by a car dealer in one month, etc.,

For instance, three responsible persons say, P₁, P₂, and P₃ are asked about their opinion in favour of building a model school in a certain district. Each person’s response is recorded as Yes (Y) or No (N). Determine the random variable that could be of interest in this regard. The possibilities of the response are as follows

Form the above table, the discrete random variable take values 0, 1, 2 and 3.

Probability Mass function

Definition 6.3

If X is a discrete random variable with distinct values x₁ , x₂ , ..., x_n , ... , then the function, denoted by P_X (x) and defined by

This is defined to be the probability mass function or discrete probability function of X. The probability mass function p(x) must satisfy the following conditions

(i) p(xi )≥ 0 ∀i ,  (ii)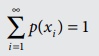 

Example 6.1

The number of cars in a household is given below.

Estimate the probability mass function. Verify p(x_i ) is a probability mass function.

Solution:

Let X be the number of cars

Hence p (x_i)is a probability mass function.

Note

For X = 0 , the probability 0.03, comes from 30/1000, the other probabilities are estimated similarly.

Example 6.2

A random variable X has the following probability function

(i) Find a , Evaluate (ii) P (X < 3) , (iii) P (X > 2) , and (iv) P (2 < X ≤ 5) .

Solution:

Example 6.3

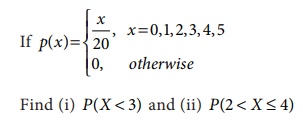
Solution:

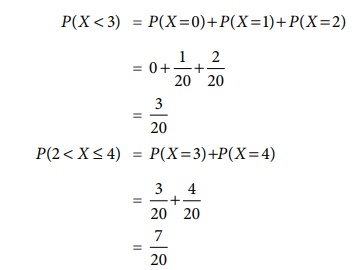
Example 6.4

If you toss a fair coin three times, the outcome of an experiment consider as random variable which counts the number of heads on the upturned faces. Find out the probability mass function and check the properties of the probability mass function.

Solution:

Let X is the random variable which counts the number of heads on the upturned faces. The outcomes are stated below

These values are summarized in the following probability table.

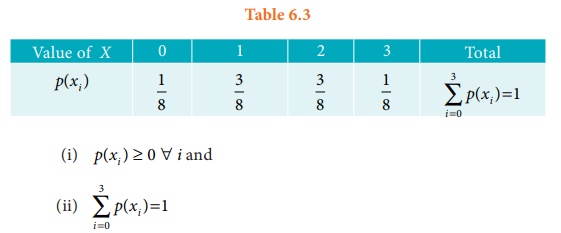
(i) p (x_i) ≥ 0 ∀ i 

Hence, p(x_i)is a probability mass function.

Example 6.5

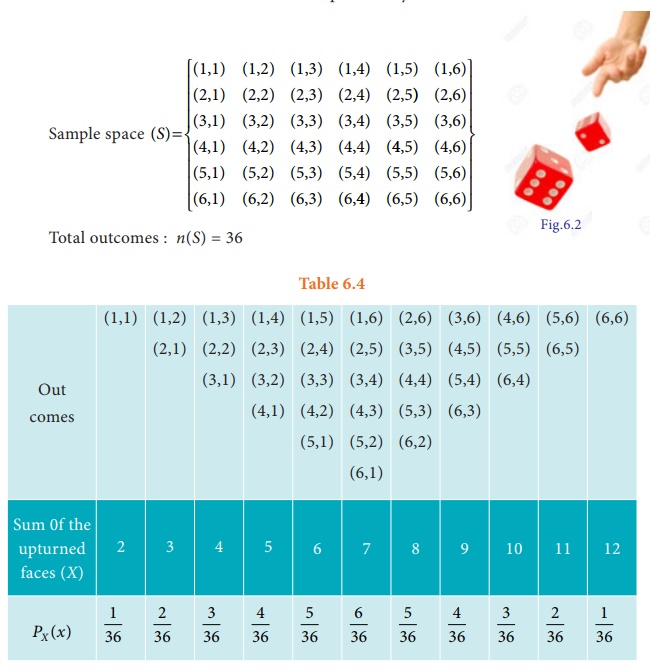
Two unbiased dice are thrown simultaneously and sum of the upturned faces considered as random variable. Construct a probability mass function.

Solution:

Discrete distribution function

Definition 6.4

The discrete cumulative distribution function or distribution function of a real valued discrete random variable X takes the countable number of points x₁ , x ₂ , ... with corresponding probabilities p(x₁ ), p(x₂ ), ... and then the cumulative distribution function is defined by

F_X (x) = P (X ≤ x ), for all x ∈R

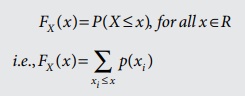
For instance, suppose we have a family of two children. The sample space

S = {bb, bg, gb, gg}, where b =boy and g = girl

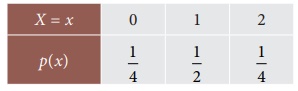
Let X be the random variable which counts the number of boys. Then, the values (X) corresponding to the sample space are 2, 1, 1, and 0.

Hence, the probability mass function of X is

Then, we can form a cumulative distribution function of X is

Example 6.6

A coin is tossed thrice. Let X be the number of observed heads. Find the cumulative distribution function of X .

Solution:

The sample space (S) ={ (HHH), (HHT), (HTH), (HTT),(THH),(THT),(TTH),(TTT)}

X takes the values: 3, 2, 2, 1, 2, 1, 1, and 0

Example 6.7

Construct the distribution function for the discrete random variable X whose probability distribution is given below. Also draw a graph of p(x) and F(x).

Solution:

From the values of p (x) given in the probability distribution, we obtain

F(1) = P(x≤1) = P(1) = 0.10

F(2) = P(x≤2) = P(1) + P(2) = 0.10 + 0.12 + 0.22

F(3) = P(x≤3) = P(1) + P(2) + P(3)

= + F(2) + P(3)

 = 0.22 + 0.20

 = 0.42

F(4) = F(3) + P(4)

=  0.42 + 0.30

 = 0.72

F(5) = F(4) + P(5)

= 0.72 + 0.15

= 0.87

F(6) = F(5) + P(6)

= 0.87 + 0.08

= 0.95

F(7) = F(6) + P(7)

= 0.95 + 0.05

= 1.00