Definition, Formulas, Solved Example Problems - Continuous random variable | 12th Business Maths and Statistics : Chapter 6 : Random Variable and Mathematical Expectation
Chapter: 12th Business Maths and Statistics : Chapter 6 : Random Variable and Mathematical Expectation
Continuous random variable
Continuous
random variable
Definition 6.5
A random variable X
which can take on any value (integral as well as fraction) in the interval is
called continuous random variable.
Examples of continuous random variable
·
The amount of water in a 10 ounce bottle.
·
The speed of a car.
·
Electricity consumption in kilowatt hours.
·
Height of people in a population.
·
Weight of students in a class.
·
The length of time taken by a truck driver to go from Chennai to
Madurai, etc.
Probability density function
Definition 6.6
The probability that a
random variable X takes a value in the interval [t1 , t2
] (open or closed) is given by the integral of a function called the
probability density function
f X (x)
:
P ( t1 ≤ X ≤t2 )= t2∫t1 f X (x)dx .

Other names that are
used instead of probability density function include density function,
continuous probability function, integrating density function.
The probability density
functions f X (x) or simply by f (x)
must satisfy the following conditions.
(i)
f ( x) ≥ 0 ∀ x and
(ii) ∞∫-∞ f (x)dx = 1 .
Example 6.8
A continuous random
variable X has the following p.d.f
f (x) = ax , 0 ≤ x ≤ 1
Determine the constant a
and also find P [X
≤ 1/2]
Solution:
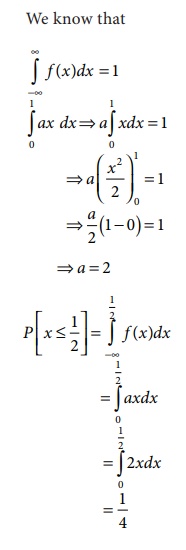
Example 6.9
A continuous random
variable X has p.d.f
f(x) =
5x 4 ,0 ≤
x ≤ 1
Find a1
and a2 such that (i) P[X
≤ a1 ] = P[X > a1] (ii) P[X > a2 ] = 0.05
Solution

Continuous distribution function
Definition 6.7
If X is a
continuous random variable with the probability density function fX
(x), then the function FX (x) is defined by
FX (x) = P[X ≤ x ] = x∫-∞ f (t )dt ,
−∞ < x < ∞ is called the distribution function (d.f) or sometimes the cumulative
distribution function (c.d.f) of the continuous random variable X
Properties of cumulative distribution function
The function FX(x)
or simply F(x) has the following properties
(i) 0 ≤ F (x) ≤ 1, − ∞ < x < ∞
(ii) 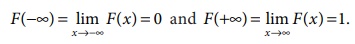
(iii) F(⋅) is a monotone,
non-decreasing function; that is, F (a)≤ F (b) for
a <b .
(iv) F(⋅) is continuous
from the right; that is, 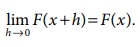
(v) 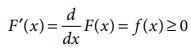
(vi) 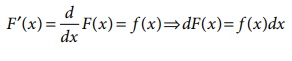
dF(x) is
known as probability differential of X .
(vii) 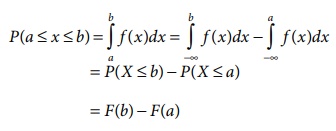
= P (X ≤ b) − P(X ≤ a)
= F (b) − F (a)
Example
6.10
Suppose, the life in
hours of a radio tube has the following p.d.f
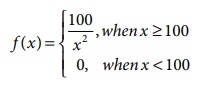
Find the distribution
function.
Solution:

Example
6.11
The amount of bread (in
hundreds of pounds) x that a certain bakery is able to sell in a day is found
to be a numerical valued random phenomenon, with a probability function
specified by the probability density function f (x) is given by

(a) Find the value of A.
(b) What is the
probability that the number of pounds of bread that will be sold tomorrow is
(i) More than 10 pounds,
(ii) Less than 10
pounds, and
(iii) Between 5 and 15
pounds?
Solution:
(a) We know that
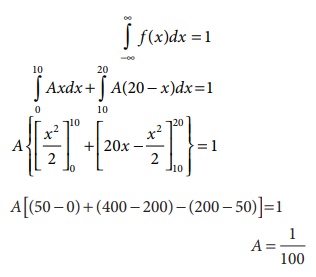
(b) (i) The probability that the
number of pounds of bread that will be sold tomorrow is more than 10 pounds is
given by
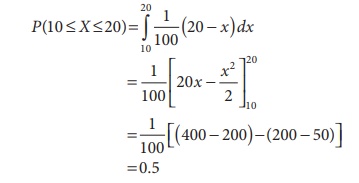
(ii) The probability that the number of pounds of bread that will be sold tomorrow is less than 10 pounds, is given by
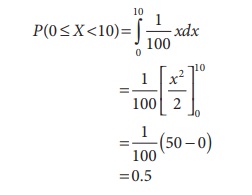
(iii) The probability that the number of pounds of bread that will be sold tomorrow is between 5 and 15 pounds is
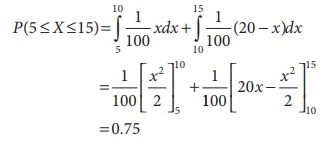
Related Topics