Definition, Formulas | Mathematical Expectation - Expected value and Variance | 12th Business Maths and Statistics : Chapter 6 : Random Variable and Mathematical Expectation
Chapter: 12th Business Maths and Statistics : Chapter 6 : Random Variable and Mathematical Expectation
Expected value and Variance
Expected
value and Variance
Expected value
The expected value is a
weighted average of the values of a random variable may assume. The weights are
the probabilities.
Definition 6.8
Let X be a
discrete random variable with probability mass function (p.m.f.) p(x)
. Then, its expected value is defined by
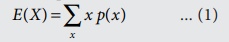
If X is a
continuous random variable and f(x) is the value of its
probability density function at x, the expected value of X is
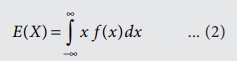
Note
In (1), E(X) is defined
to be the indicated series provided that the series is absolutely convergent;
otherwise, we say that the mean does not exist.
In (1), E(X) is an
“average” of the values that the random variable takes on, where each value is
weighted by the probability that the random variable is equal to that value.
Values that are more probable receive more weight.
In (2), E(X) is defined
to be the indicated integral if the integral exists; otherwise, we say that
the mean does not exist.
In (2), E(X) is an
“average” of the values that the random variable takes on, where each value x is
multiplied by the approximate probability that X equals the value x,
namely f X (x)dx and then integrated
over all values.
Variance
The variance is a
weighted average of the squared deviations of a random variable from its mean.
The weights are the probabilities. The mean of a random variable X,
defined in (1) and (2), was a measure of central location of the density of X.
The variance of a random variable X will be a measure of the spread or
dispersion of the density of X or simply the variability in the values
of a random variable.
Definition 6.9
The variance of X
is defined by
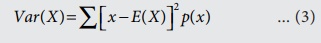
if X is
discrete random variable with probability mass function p(x).
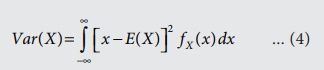
if X is
continuous random variable with probability density function f X
(x) .
Definition 6.10
Expected value of [X
–E(X)]2 is called the variance of the random variable.
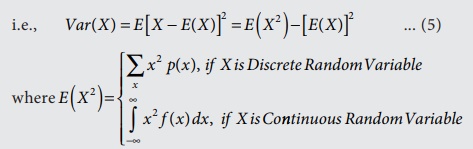
Note
·
In the following examples, variance will be found using
definition 6.10.
·
The variances are defined only if the series in (3) is
convergent or if the integrals in (4) exist.
·
If X is a random variable, the standard deviation of X (S.D(X)),
denoted by σX , is defined as 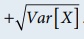
·
The variance of X , denoted by σX2
or Var(X) or V(X)
Related Topics