Chapter: 12th Business Maths and Statistics : Chapter 6 : Random Variable and Mathematical Expectation
Mathematical Expectation: Solved Example Problems
Example
6.12
Determine the mean and
variance of the random variable X having the following probability
distribution.

Solution:
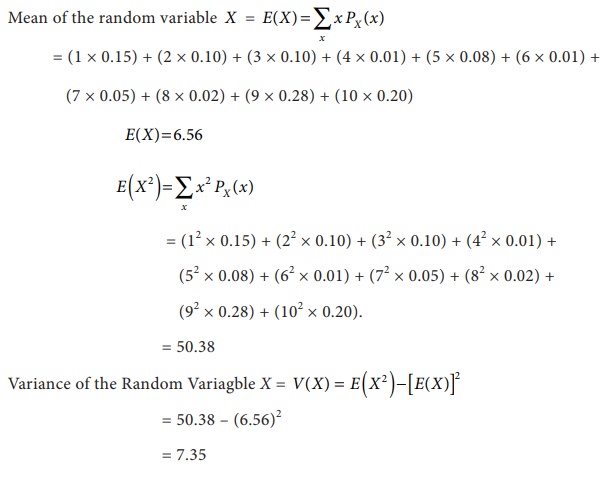
Therefore, the mean and variance of
the given discrete distribution are 6.56 and 7.35 respectively.
Example
6.13
Six men and five women
apply for an executive position in a small company. Two of the applicants are
selected for an interview. Let X denote the number of women in the interview
pool. We have found the probability mass function of X.
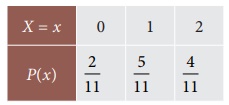
How many women do you
expect in the interview pool?
Solution:
Expected number of women
in the interview pool is
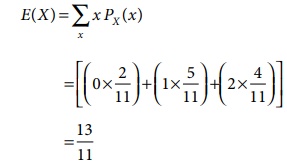
Example
6.14
Determine the mean and
variance of a discrete random variable, given its distribution as follows:
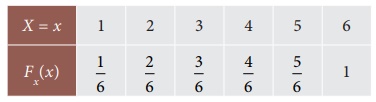
Solution
From the given data, you
first calculate the probability distribution of the random variable. Then using
it you calculate mean and variance.

Example
6.15
The following
information is the probability distribution of successes.
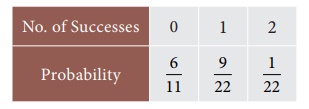
Determine the expected
number of success.
Solution
Expected number of
success is
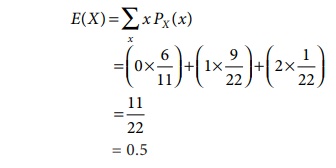
Therefore, the expected
number of success is 0.5. Approximately one success.
Example
6.16
An urn contains four
balls of red, black, green and blue colours. There is an equal probability of getting any coloured ball. What
is the expected value of getting a blue ball
out of 30 experiments with replacement?
Solution
Probability of getting a
blue ball = (p) = 1/4 = 0.25
Total experiments (N) =
30
Expected value = Number
of experiments × Probability
= N × p
= 30 × 0.25
= 7.50
Therefore, the expected value of getting blue ball is approximately 8.
Example
6.17
A fair die is thrown.
Find out the expected value of its outcomes.
Solution
If the random variable X
is the top face of a tossed, fair, six sided die, then the probability mass function of X is
Px (x)= 1/6, for x = 1,2,3,4,5 and 6
The average toss, that
is, the expected value of X is

Therefore, the expected toss of a fair six sided die is 3.5.
Example
6.18
Suppose the probability
mass function of the discrete random variable is
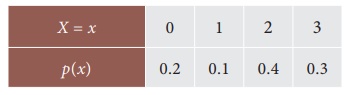
What is the value of E(3X
+ 2X2) ?
Solution

Example
6.19
Consider a random
variable X with probability density function
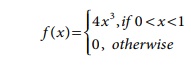
Find E(X) and V(X).
Solution
We know that,
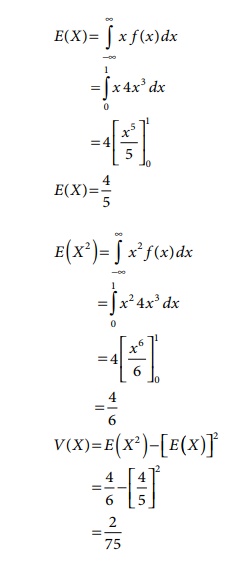
Example
6.20
If f (x)
is defined by ( x) =
ke−2 x , 0
≤ x < ∞ is a density function.
Determine the constant k and also find mean.
Solution
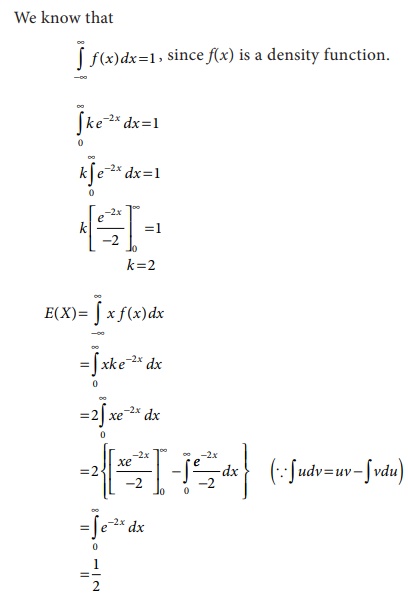
Example
6.21
The time to failure in
thousands of hours of an important piece of electronic equipment used in a
manufactured DVD player has the density function.
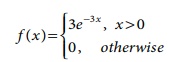
Find the expected life
of the piece of equipment.
Solution:
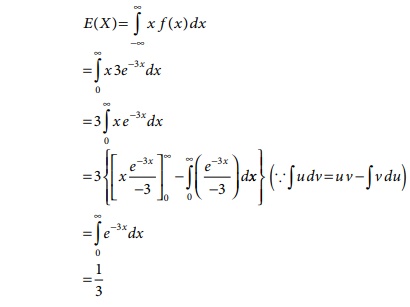
Therefore, the expected life of the
piece of equipment is 1/3 hrs (in
thousands).
Example
6.22
A commuter train arrives
punctually at a station every 25 minutes. Each morning, a commuter leaves his
house and casually walks to the train station. Let X denote the amount
of time, in minutes, that commuter waits for the train from the time he reaches
the train station. It is known that the probability density function of X
is
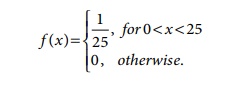
Obtain and interpret the
expected value of the random variable X.
Solution:
Expected value of the
random variable is
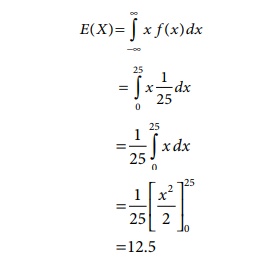
Therefore, the expected waiting time of the commuter is 12.5 minutes.
Example
6.23
Suppose the life in
hours of a radio tube has the probability density function
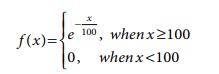
Find the mean of the
life of a radio tube.
Solution:
We know that, the
expected random variable

Therefore, the mean life of a radio
tube is 7,358 hours.
Example
6.24
The probability density
function of a random variable X is
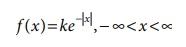
Find the value of k and
also find mean and variance for the random variable.
Solution:
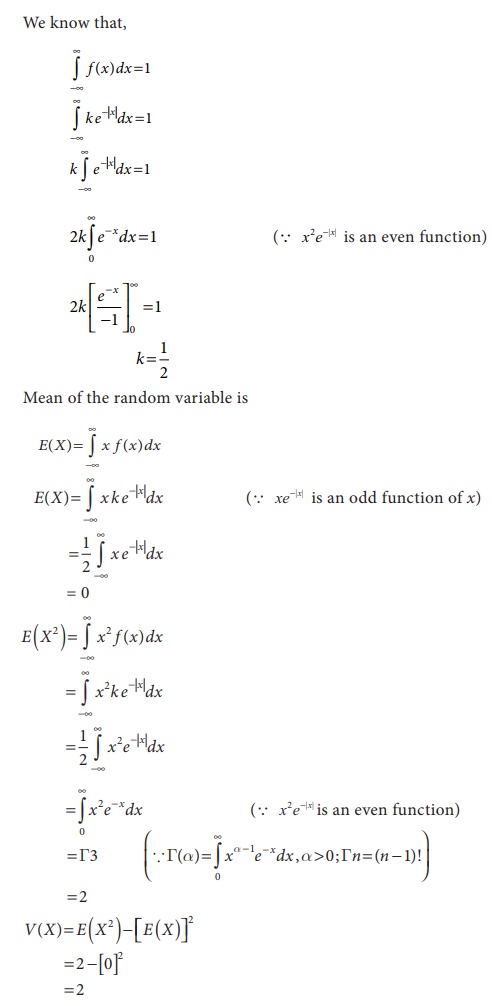
Related Topics