Identification of Recombinants - Recombinant DNA Technology

Identification of Recombinants

Once a recombinant DNA molecule has been introduced into appropriate host cells, it becomes imperative to select only those cells which have the rDNA from those of the original host cells which have not taken up the DNA. All procedures described in the previous section are only minimally efficient (about 1%) and hence after such an experiment majority of the cells do not have the foreign DNA. However the use of selectable marker genes which are an integral part of any cloning vector makes the selection of transformed cells quite easy. Generally, the selection methods are based on the expression or non-expression of certain traits such as antibiotic resistance, expression of an enzyme such as β-galactosidase or protein such as GFP (Green Fluorescent Protein) and dependence or independence of a nutritional requirement such as the amino acid leucine. For example if the host E. coli cells have taken up the plasmid pBR322 then these cells will grow in media containing the antibiotics ampicillin or tetracycline whereas normal E. coli cells will be killed by the antibiotics. Thus only transformed cells, however few, will be selected for growth and division.

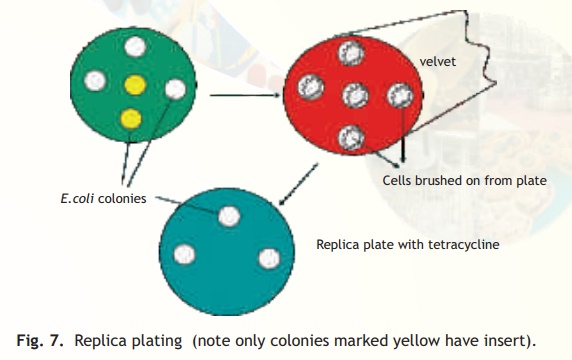
The simplest method for selecting the transformants relies on the presence of antibiotic resistance genes on the plasmid or phage based vectors as already discussed. It is possible however, that the transformants have the vector without the foreign DNA. This is because the procedure for making a recombinant vector is efficient but not 100% foolproof! If on the other hand a vector has two antibiotic resistant genes, e.g. pBR322, and the insert is contained in the tetracycline resistant gene, then the ampicillin resistant gene will be normally expressed allowing the transformed cells to grow on an ampicillin containing medium but due to a phenomenon called insertional inactivation (insert in tetracycline gene) the cells will be tetracycline sensitive. How does a scientist select for a sensitive or negative trait following a transformation experiment? A procedure called replica plating is used. As schematically explained in Fig. 7 following an experiment of transforming E. coli cells with recombinant pBR322 plasmid, the host cells are first plated on solid media (agarose containing) with the antibiotic ampicillin (assume that the insert has been ligated within the tetracycline resistance gene). Colonies from every single cell plate having the plasmid will develop overnight. The role of the recombinant plasmid is to help the cell to multiply in the presence of antibiotic, which it would otherwise not be able to do. In order to select those colonies alone which are tetracycline sensitive and therefore, are relevant to the experiment as they have the insert, a procedure called replica plating is used. A petri plate containing solid media with antibiotic tetracycline is kept carefully under asceptic conditions(Laminar flow hood) to which a circular piece of velvet or velvet paper is aligned and pressed onto the colony containing ampicillin plate (master plate). With the same alignment it is pressed onto the tetracycline plate. Overnight only colonies not containing the insert will grow while due to insertional inactivation no colonies will grow which have the insert. The colonies which have the insert can easily be scored off by comparing the two plates.

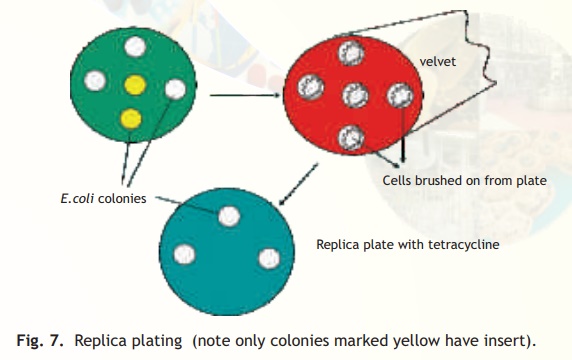
Fig. 7.  Replica plating  (note only colonies marked yellow have insert).

Another powerful method of screening for the presence of recombinant plasmids is referred to as blue- white selection. This method is based upon the insertional inactivation of the lac Z gene present on the vector (e.g. pUC 19). This gene expresses the enzyme β-galactosidase whose activity can cleave a colourless substrate called X-Gal into a blue coloured product. If the lac Z gene is inactivated due to the presence of the insert then the enzyme is not expressed. Hence if after a transformation experiment the E. colihost cells are plated on an ampicillin and X-Gal containing solid media plate then colonies which appear blue are those which have transformed cells (antibiotic resistant) but do not have the insert (express active enzyme). Colonies which appear white are both ampicillin resistant and have the insert recombinant DNA and thus are the cells to be used for future experiments.

The above described methods are used for selection of E. coli recombinants. There are several methods used for other host cell recombinants but the principles remain the same. Furthermore techniques for actually detecting recombinant proteins from colonies also have to be used where relevant. Where amplification of the insert DNA is the primary objective, plasmids are isolated from the host cells after growing the latter in large amounts and using the same restriction enzyme the insert is cut from the plasmid and recovered after electrophoresis.