Chapter: Physics : Crystal Physics
Hexagonal Closely Packed Structure(HCP)
Hexagonal Closely Packed
Structure(HCP)
The
hexagonal closely packed (hcp) is shown in the figure 1.1.8. In the hcp
structure of an unit cell contains three types of atoms as three layers.

12
corner atoms, one at each and every corner of the Hexagon.
2
base centered atoms, one at the top face of the hexagon and another at the
bottom face of the hexagon.
In
addition to corner and base atoms, 3 atoms are situated in between the top and
bottom face of the hexagon, in alternate vertical faces. Also note that these
atoms are situated inside the face so that they can’t be shared by other cells
as shown in the figure .1.10
(i)
Number
of atoms per unit cell
To
calculate the number of atoms per unit cell, first consider the bottom layer.
The bottom layer consists of six corner atoms and one face centered atom. Each
and every corner atom contributes 1/6 of its part to one unit cell. The total
number atoms contributed by the corner atoms is 1/6 x 6 = 1. The face-centered
atom contributes ½ of its part to one unit cell. Therefore, the total number of
atoms contributes ½ of its part to one unit cell. Therefore, total number of
atoms present in the case of the bottom layer is 1 + ½ = 3/2
Similarly,
the number of atoms present in the upper layer is 1 + ½ = 3/2
The
number of the atoms present in the middle layer = 1 x 3 = 3
The
total number of atoms present in the unit cell = 3/2 + 3/2 + 3 = 6 atoms.
(ii)
Atomic
Radius
To
find the atomic radius of the hcp structure, consider any two-corner atoms. It
has to be noted that, each and every corner atom touches with each other,
therefore they are nearest neighbor.
From
figure 1.1.8.1 we can write
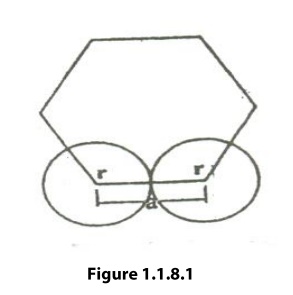
Atomic
Radius – HCP Structure
(iii)
Coordination
Number
The
coordination number of the hcp structure can be calculated as follows. Let us
consider two unit cells as shown in the figure 1.1.8.2
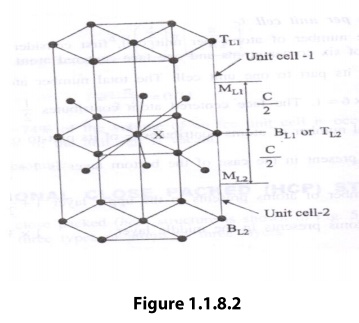
The
hcp structure is considered to have three layers viz, 1) Bottom Layer [B1],2)
Top Layer [T1] and 3) Middle Layer [M1] as shown.
In
the top and bottom layers, the base centered atom is surrounded by six corner
atoms. In the middle layer we have 3 atoms stacked inside the unit cell as
shown. Let us consider two unit cells let ‘X’ be the reference atom taken in
the bottom layer BL1 of unit cell 1(or top layer [TL2] of unit cell 2). This
atom has 6 neighboring atom in its own plane. Further at a distance of c/2 it
has 3 atoms in the middle layer (ML1) of unit cell -1 and 3 more atoms in the
middle layer (ML2) of unit cell -2. Therefore, the total number of neighboring
atoms is 6+3+3=12
Thus
the coordination number is 12.
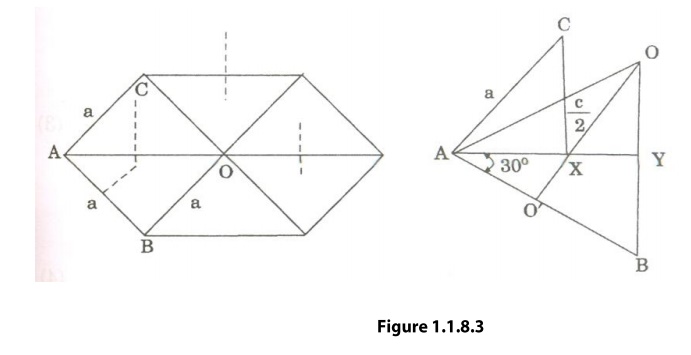
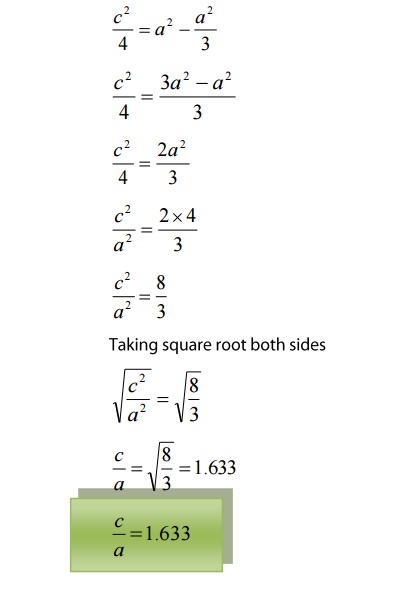
We
know that ‘c’ is the height of the unit cell of HCP structure and ‘a’ is the
distance between two neighboring atoms. Now consider a triangle ABO in the
bottom layer.
Here
A,B, and O are the lattice points and exactly above these atoms at a
perpendicular distance ‘c’/2 the next layer atom lies at C.
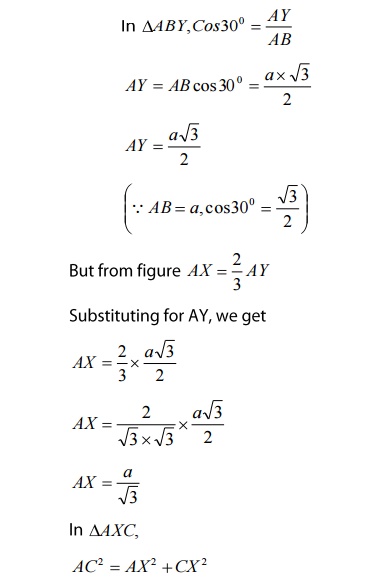
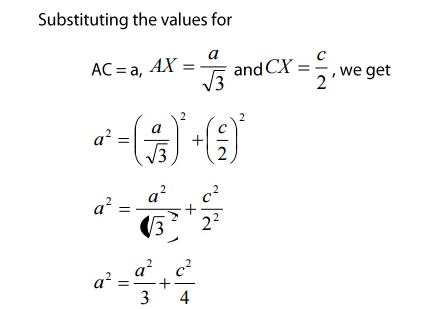
(iv)
Atomic
Packing factor
Volume
of all atoms in a unit cell(v)
Atomic
radius r = a/2
No
of atoms per unit cell, n =6
Volume
of all the six atoms in the unit cell

The
volume of the unit cell of the HCP = base area x height

Thus
the packing density is 74% and hence, it is a closed packed structure.
Example.
Zinc, Beryellium and Magnesium
Related Topics