Gas Liquid Chromatography (GLC): Theory

THEORY

There are, in fact, three theories that have gained virtually wide recognition and acceptance in describ-ing a gas chromatographic separation, namely :

(a) Plate theory,

(b) Rate theory, and

(c) Random walk and nonequilibrium theory.

These different theories will be discussed briefly in the sections that follows :

1. PLATE THEORY

Martin and Synge* first proposed the ‘plate theory’ in 1941, whereby they merely compared the GC separation to fractional distillation. Thus, the ‘theoretical’ plate is the portion of the column wherein the solute is in complete equilibrium with the mobile and the stationary phase.

This equilibrium is represented by the following expression :

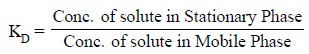
where,  K_D = Distribution coefficient.

Thus, the distribution of a solute after ‘n’ equilibrium (plates) may be defined by the expansion of the binomial in Eq. (a) below :

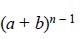              .........................(a)

where, (n – 1) = Number of transfers between the plates,

a = 1/(K_D + 1), and

b = K_D/(K_D + 1).

2. RATE THEORY

As the ‘Plate Theory’ has two serious limitation, viz., first : it does not speak of the separating power of a definite length of column, and second : it does not suggest means of improving the performance of the column ; the ‘Rate Theory’ has been introduced which endeavours to include the vital fact that-‘the mobile-phase flows continuously, besides the solute molecules are constantly being transported and partitioned in a gas chromatographic column’. It is usually expressed by the following expression :

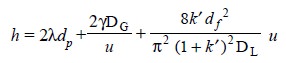                 .......................(b)

where, u = Average linear gas velocity,

λ= Measure of the packing irregularities

d_p = Particle diameter,

γ= Tortuosity factor,

D_G = Coefficient of gaseous diffusion of the solute in the carrier gas,

k′ = Ratio of the amount of solute in the stationary phase to that in the gas phase, d_f = Film thickness (usually in µm), and

D_L = Diffusion constant of solute in liquid phase.

Eq. (b) was first advocated by Van Deemter* in 1956, and may be rewritten as given below [Eq. (c)] wherein all terms except ‘u’ are constant :

          ........................(c)

3 RANDOM WALK AND NONEQUILIBRIUM THEORY

Giddings** in 1958, first proposed the captioned theory wherein he suggested a chromatographic separation in terms of a random walk. Based on a statistical concept the virtual spreading of a ‘solute band’ may be considered by virtue of molecular diffusion, mass transfer, and Eddy diffusion (i.e., flow pattern effects) were equated to standard deviation. In fact, this particular approach correlates the spreading of a chromatographic peak to various parameters, for instance : mass transfer, diffusion coefficient D_G, particle diameter, velocity of mobile-phase, and finally the length of column. Thus, coefficient D_G, particle diameter, velocity of mobile-phase, and finally the length of column. Thus, the plate height ‘h’ employing the random walk approach may be expressed as in Eq. (d) :

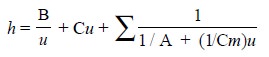             .....................(d)

where, Cm = Resistance to mass transfer in gas phase should be treated independently,

A = Eddy diffusion,

B = Longitudinal molecular diffusion in both mobile and stationary phases, and

C = Kinetic or mass transfer term originating in the stationary phase.

In actual practice, there are two basic considerations that prevail upon in gas chromatography, namely :

(a) Retention : The phenomena affecting retention or hold up on the column, sometimes referred to as the thermodynamic effect, and

(b) Column Efficiency : The phenomena affecting column efficiency or the kinetic aspect that governs the tendency for a particular solute band to ‘broaden’ as it traverses through the column.

However, the resolution or extent of separation of any two peaks from a column is solely dependent upon both retention and column efficiency.

Although separations may be caused by elution, frontal and displacement analyses, yet the elution technique is the most common. This method makes use of a stream of carrier-gas flowing through the column. Precisely, a sample is injected into the carrier-gas as a ‘plug’ of vapour that is swept into the head of the packed chromatographic column. Separation of components that comprise the sample results from a difference in the multiple forces by which the column materials tend to retain each of the components.

Irrespective of the nature of the retention that is due to adsorption, solubility, chemical binding, polarity or molecular filtration, the column does retain some components longer than others. When in the gas phase the components are moved toward the column outlet, they are selectively retarded by the station-ary phase. Consequently, all components pass through the column at varying speeds and emerge in the inverse order of their retention by the column materials. 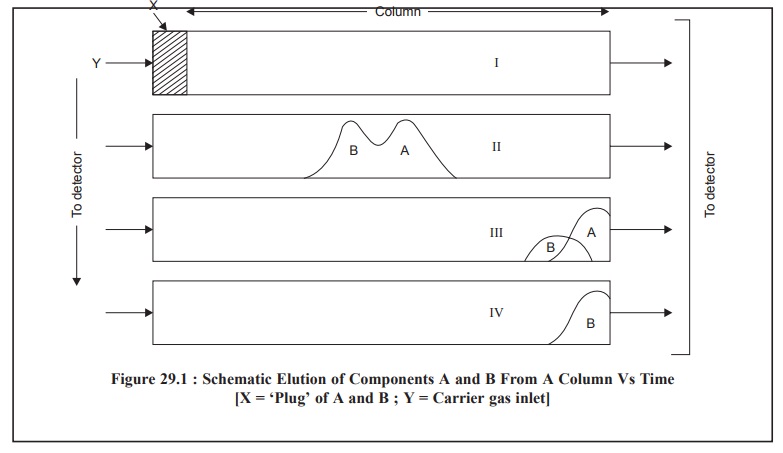The aforesaid process may be outlined schematically as shown in Figure 29.1

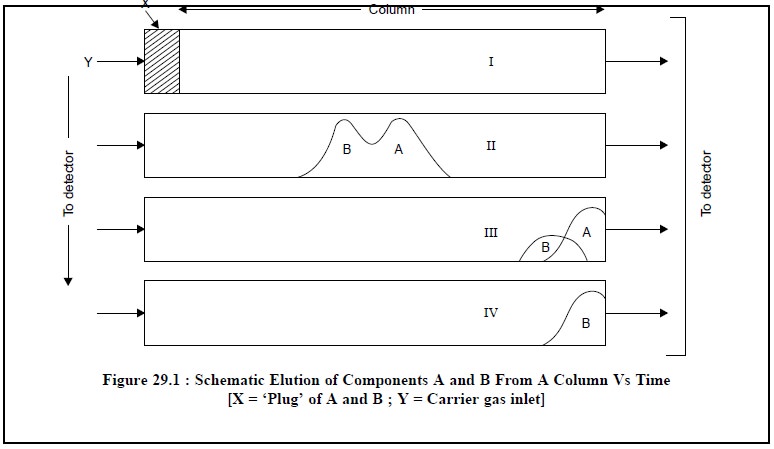
Upon emerging from the column, the gaseous phase immediately enters a ‘detector’ attached to the column. Here, the individual components register a series of signals that appear as a succession of peaks above a base line on the chromatogram.

From Figure 29.1, it is evident that ‘plug’ of mixture A and B just enters the column 1 at time T₁, moves to the middle of the column I at time T₂, part of A has passed through the column III at time T₃ and finally A has passed completely and part of B passed through the column IV at time T₄.