Formal Methods

Formal Methods

What Are Formal Methods

•      Formal methods refers to a variety of mathematical modeling techniques that are applicable to computer system design.

•      They include activities such as system specification, specification analysis and proof, transformational development, and program verification.

Definition

“  Formal methods are mathematical approaches to software and system development which support the rigorous specification, design and verification of computer systems.” ^[Fme04]

  “[they]… exploit the power of mathematical notation and mathematical proofs. “ ^[Gla04]

Seven Myths of Formal Methods

1.     Formal methods can guarantee that software is perfect.

2.     Work by proving that programs are correct.

3.     Only highly critical systems benefit from their use.

4.     They involve complex math.

5.     They increase the cost of development.

6.     They are incomprehensible to clients.

7.     Nobody uses them for real projects.

History

•      Formal specifications have been in use since the early days of computing.

–     1940's:        Turing annotated the properties of program states to simplify the logical analysis of  sequential programs.

–     1960's:        Floyd, Hoare and Naur recommended using axiomatic techniques to prove programs meet their  specifications.

–     1970's:        Dijkstra used formal calculus to aid to develop of non-deterministic programs.

•      The interest in the use of formal methods in software engineering has continued to grow.

Definition

"Formal is often confused with precise".

      A formal specification consists of three components:

                               i.            Syntax - grammatical rules to determine if sentences are well formed

                             ii.            Semantics - rules for interpreting the sentences in a precise, meaningful way within the domain

                          iii.            Proof Theory - rules for inferring useful information from the specification

  What are Formal Methods?

§  Notation with precise syntax and semantics

§  Doesn’t necessarily involve mathematics

§  Although mathematics is a formal notation

§  There are levels of formulization.

§  Techniques, methods, procedures, tools can support levels

Types of Formal Methods

A variety of formal methods exist:

–     Abstract State Machines - The Abstract State Machine (ASM) thesis implies that any algorithm can be modeled by an appropriate ASM.

–     B-Method - B is a formal method for the development of program code from a specification in the Abstract Machine Notation.

–     Z – A specification language used for describing computer-based systems; based set theory and first order predicate logic

–     “Unified Modeling Language (UML) provides system architects…with one consistent language for specifying, visualizing, constructing, and documenting the artifacts of software systems..”

•      Visual notation for OO modeling

•      Extensible

•      Independent of programming languages

•      Formal basis for understanding the modeling language

Other Types of Formal Methods

Others types include:

–     CommUnity

–     Estelle

–     Esterel

–     Lotos

–     Overture Modeling Language

–     Petri Nets

–     RAISE

–     SDL

–     TRIO, Unity, and VDM

–     Any programming language

Predicate Calculus

•      The first order predicate calculus is a formal language for expressing propositions.

•      A properly-formed predicate calculus expression is called a well-formed formula or WFF (pronounced wiff).

•      Constant

•      Variable

•      Predicate

•      Function

•      Connective

•      Quantifier

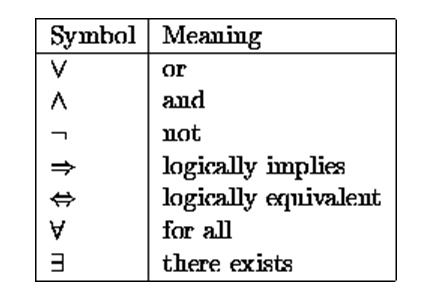
1.     Whoever can read is literate.

2.     Dogs are not literate.

3.     Some dogs are intelligent.

4.     Some who are intelligent cannot read.

1. "x [R(x) ÞL(x)]

2. "x [D(x) ÞØR(x)]

3. $x [D(x) Ù I(x)]

4. $x [I(x) ÙØ R(x)]

Do we really need Formal Methods?

Design errors

Potential causes of failure include:

–     physical failure

–     human error

–     environmental factors

–     design errors

- Design errors are the major culprit.

The promise of Formal Methods

Formal methods are needed to:

–     Improve SW Quality

–     Reduce cost of verifying system

–     Improve quality and rigor of entire development process

–     Reduce specification errors and provide a rational basis for choosing test data

–     Explore the properties of a design architecture

Weaknesses in Formal Methods

•      Weaknesses:

–     Low-level ontologies

–     Limited Scope

–     Isolation

–     Cost

–     Poor tool feedback

Success of Formal Methods

          There are many examples of successful and cost-effective systems implemented using formal methods. 

–     Mainly in domain of transportation systems

–     Also in domains such as:

•      information systems

•      telecommunication systems

•      power plant control

•      security