Exercise 5.6

Exercise 5.6

Miscellaneous Practice problems

1. Find the value of x if ∠AOB is a right angle.

Answer: 

∠AOC + ∠COB = 90°

 2x + 3x = 90°

 5x = 90°

 x = 90° / 5 = 18°

 x = 18°

2. In the given figure, find the value of x.

Answer: 

∠BOC + ∠AOC = 180°

 2x + 23 + 3x – 48 = 180°

 5x – 25 = 180°

 5x = 180° + 25^o

 = 205^o

 x = 205^o / 5 = 41°

 x = 41°

3. Find the value of x, y and z

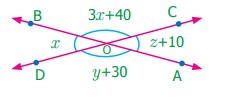
Answer: 

∠BOD + ∠BOC = 180°

 x + 3x + 48 = 180°

 4x + 40 = 180°

 4x = 180° – 40^o

 = 140^o

x = 140^o / 4 = 35°

 x = 35°

∠BOD + ∠AOD = 180°

 x + y + 30° = 180°

 35° + y + 30° = 180°

 y = 180° – 65^o

 y = 115^o

∠AOD + ∠AOC = 180°

y + 30° + z + 10° = 180°

 115° + z + 40° = 180°

 z + 155° = 180°

z = 180° – 155° = 25°

z = 25° 

4. Two angles are in the ratio 11: 25. If they are linear pair, find the angles.

Answer: 

Two angles are in the ratio 11:25

Let the two angles be 11x, 25x

Sum of two angles 11x + 25x = 180°

36x = 180°

   x = 180^o / 36 = 5°

    x = 5°

11x = 11 × 5° = 55°

25x = 25 × 5° = 125°

The two angles are 55^o, 125^o

5. Using the figure, answer the following questions and justify your answer.

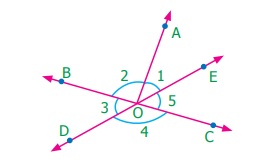
(i) Is ∠1 adjacent to ∠2?

(ii) Is ∠AOB adjacent to ∠BOE?

(iii) Does ∠BOC and ∠BOD form a linear pair?

(iv) Are the angles ∠COD and ∠BOD supplementary?

(v) Is ∠3 vertically opposite to ∠1?

(i) Is ∠l adjacent to ∠2?

Yes. They have a common vertex, a common arm and their interiors do not overlap.

(ii) Is ∠AOB adjacent to ∠BOE?

No. They have overlapping interiors.

(iii) Do ∠BOC and ∠BOD form a linear pair?

No. Since ∠BOC is a straight angle, their sum will exceed 180°.

(iv) Are ∠COD and ∠BOD supplementary?

Yes. They are linear pair.

(v) Is ∠3 vertically opposite to ∠1 ?

No. They are not formed by intersecting lines.

6. In the figure POQ, ROS and TOU are straight lines. Find the x°.

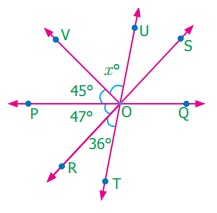
Answer: 

∠UOV + ∠VOP + ∠POR + ∠ROT = 180°

x + 45° + 47° + 36° = 180°

x + 128° = 180° 

x = 180° – 128° = 52°

x = 52^o

7. In the figure AB is parallel to DC. Find the value of ∠1 and ∠2. Justify your answer.

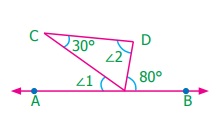
Answer: 

From the figure, ∠DCE = ∠1 (alternate angles)

30° = ∠l

∠l = 30°

∠2 = ∠DEB (alternate angles)

∠2 = 80°

8. In the figure AB is parallel to CD. Find x,y and z.

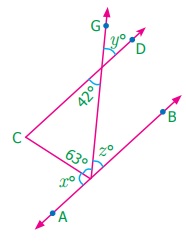
Answer: 

From the figure,

∠GED = ∠CEF (vertically opposite angles)

y = 42°

∠CEF = ∠EFB (alternate angles)

42° = ∠z

∠z = 42°

∠AFC + ∠CFE + ∠EFB = 180°

x° + 63°+ z° = 180°

x° + 63° + 42° = 180°

x° + 105° =180°

x° = 180°– 105° = 75°

x° = 75°

x° = 75°, y = 42°, z = 42°

9. Draw two parallel lines and a transversal. Mark two alternate interior angles G and H. If they are supplementary, what is the measure of each angle?

Answer: 

Angles G and H are supplementary

∠G and ∠H are alternate interior angles.

 ∴ ∠G = ∠H = 90° 

10. A plumber must install pipe 2 parallel to pipe 1. He knows that ∠1 is 53. What is the measure of ∠2?

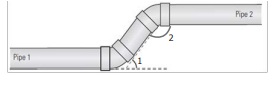
Answer: 

∠1 + ∠2 = 180°

53° + ∠2 = 180°

∠2 = 180° – 53° = 127°

∠2 = 127°

Challenge Problems

11. Find the value of y.

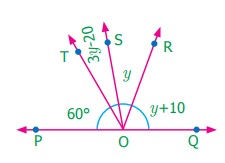
Answer: 

∠POT + ∠TOS + ∠SOR + ∠ROQ = 180^o

60° + 3y – 20 + y + y + 10 = 180°

60° + 10 – 20 + 5y = 180°

 70 – 20 + 5y = 180°

 50 + 5y = 180°

 5y = 180° – 50° = 130°

 y = 130° / 5 = 26^o

 y = 26°

12. Find the value of z.

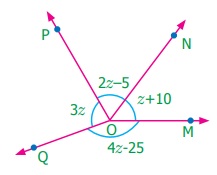
Answer: 

∠POQ + ∠QOM + ∠MON + ∠PON = 360^o

3z + 4z –25 + z + 10 +2z – 5 = 360^o

 3z + 4z + z + 2z + 10 – 25 – 5 = 360^o

 10z – 20 = 360^o

 10z = 360^o + 20^o = 380^o

 z = 380^o / 10 = 38^o

 z = 38^o

13. Find the value of x and y if RS is parallel to PQ.

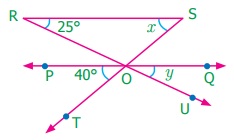
Answer: 

From the figure,

∠POR = ∠ORS (alternate angles)

∠POR = 25°

∠POR = ∠QOU (vertically opposite angles)

∠QOU = 25°

 y = 25°

∠POT = ∠SOQ (vertically opposite angles)

 40° = ∠SOQ

∠RSO = ∠SOQ (alternate angles)

x° = 40°

y° = 25°

14. Two parallel lines are cut by a transversal. For each pair of interior angles on the same side of the transversal, if one angle exceeds the twice of the other angle by 48°. Find the angles.

Answer: 

Given one angle exceeds twice of other angle by 48°

= 2x + 48

Other angle = x°

Sum of interior angles = x° + 2x° + 48° = 180°

3x + 48° = 180°

3x = 180° – 48° = 132°

x = 132^o / 3 = 44^o

x = 44°

2x + 48 = 2 × 44 + 48

 = 88 + 48° = 136°

The angles are 44°, 136°.

15. In the figure, the lines GH and IJ are parallel. If ∠1=108° and ∠2 = 123°, find the value of x, y and z.

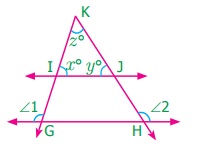
Answer: 

∠1 = 108°

Interior angle          ∠G = 180^o – 108^o = 72^o

x° = Interior angle   ∠G (corresponding angles)

x° = 72°

∠2 = 123°

Interior angle               ∠H = 180° – 123° = 57°

y° = Interior angle       ∠H = (corresponding angles)

y = 57°

x° + y° + 2° = 180° (sum of the triangles)

72° + 57° + z° = 180°

129° + z° = 180°

z° = 180° – 129° = 51°

x° = 72°, y° = 57°, z = 51°

16. In the parking lot shown, the lines that mark the width of each space are parallel. If ∠1 = (2x–3y)°, ∠2 = (x +39)°, find x and y.

Answer: 

∠2 + 65° = 180° (interior angles)

(x + 39) + 65° = 180°

x + 104° = 180°

 x = 180° – 104° = 76°

 x = 76°

∠1= 65° (vertically opposite angles)

(2x – 3y)^o = 65°

2(76^o) – 3y^o = 65°

152^o – 3y^o = 65^o

–3y° = 65° – 152° = –87^o

y = –87 / –3 = 29°

y = 29°

x = 76° , y = 29°

17. Draw two parallel lines and a transversal. Mark two corresponding angles A and B. If ∠A = 4x and ∠B = 3x + 7, find the value of x. Explain..

Answer: 

A and B are corresponding angles.

∠A = ∠B

4x = 3x + 7

4x – 3x = 7

x = 7°

18. In the figure AB is parallel to CD. Find x˚, y˚ and z˚.

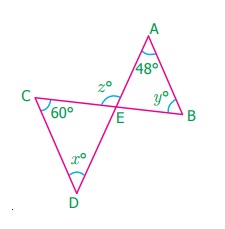
Answer: 

∠A = ∠D (alternate angles)

x° = 48°

∠C = ∠B (alternate angles)

y° = 60°

from ΔCDE,

∠C + ∠D + ∠E = 180° (sum of the three angles of a triangle)

60° + 48° + ∠E = 180°

108° + ∠E = 180°

∠E = 180° – 108°

∠E = 72°

∠E + Z° = 180°∠ (straight angles)

72° + Z° = 180°

Z° = 180° – 72° = 108°

Z° =108°

x = 48°     y = 60°    z = 108° 

19. Two parallel lines are cut by a transversal. If one angle of a pair of corresponding angles can be represented by 42˚ less than three times the other. Find the corresponding angles.

Answer: 

One angle = x

Other angle = 42 less than 3 times the other

 = 3x – 42

The corresponding angles are equal

3x – 42 = x

3x – x = 42

2x = 42

x = 21

The corresponding angles = 21

20. In the given figure, ∠8 = 107˚, what is the sum of the ∠2 and ∠4?

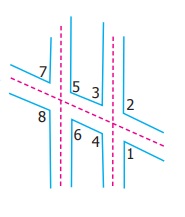
Answer: 

 ∠8 = ∠4 (Corresponding angles)

∠8 = 107°

∴ ∠4 = 107°

∠4 = ∠2 (vertically opposite angles)

∠2 = 107°

The sum of ∠2 and ∠4 = 107° + 107° = 214°. 

ANSWERS

Exercise 5.6

1. 18°

2. 41°

3. 35°, 115°, 25°

4. 55°, 125°

5. (i) Yes. They have a common vertex, a common arm and their interiors do not overlap.

(ii) No. They have overlapping interiors.

(iii) No. Since ∠BOC is a straight angle, their sum will exceed 180°.

(iv) Yes. They are linear pair.

(v) No. They are not formed by intersecting lines

6. 52°

7. 30°, 80°

8. 75° , 42° , 42°

9. 90°

10. 127°

Challenge Problems

11. 26°

12. 38°

13. 40°,25°

14. 44°

15. 72°,57°,51°

16. 76°,29°

17. 7°

18. 48°,60°,108°

19. 21°

20. 214°