Construction of special angles without using protractor

Construction of special angles without using protractor.

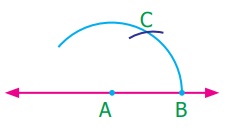
(i) Construction of angle of measure 60°

Step 1: Draw a line. Mark a point A on it.

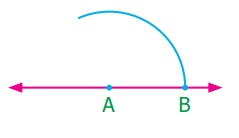
Step 2: With A as center draw an arc of convenient radius to the line to meet at a point B.

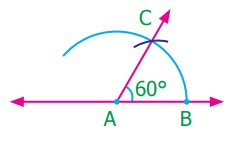
Step 3: With the same radius and B as center draw an arc to cut the previous arc at C.

Step 4: Join AC. Then ∠BAC is the required angle with the measure 60°.

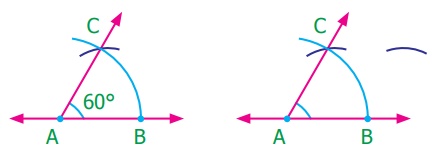
(ii) Construction of angle of measure 120°.

We know that there are two 60° agnels in 120°. Hence, to construct 120°, we can construct two 60° angles consecutively as follows.

Step 1: Draw a line. Mark a point A on it.

Step 2: With A as center, draw an arc of convenient radius to the line at a point B.

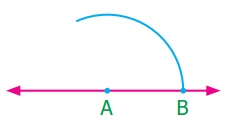
Step 3: With the same radius and B as center, draw an arc to cut the previous arc at C.

Step 4: With the same radius and C as center, draw an arc to cut the arc drawn in step 2 at D.

Step 5: Join AD. Then ∠BAD is the required angle with measure 120°.

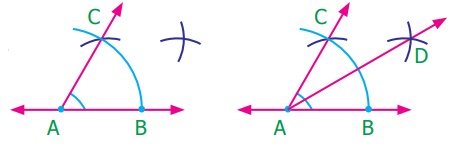
(iii) Construction of angle of measure 30°

Since 30° is half of 60°, we can construct 30° by bisecting the angle 60°.

Step 1: Construct angle 60° [Refer Construction of angle of measure 60° (i)].

Step 2: With B as center, draw an arc of convenient radius in the interior of ∠BAC.

Step 3: With the same radius and C as center, draw an arc to cut the previous arc at D.

Step 4: Join AD. Then ∠BAD is the required angle with measure 30° [Think about ∠DAC?]

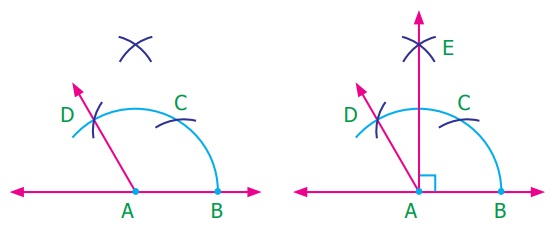
(iv) Construction of angle of measure 90°

Step 1: Construct angle 120° [Refer Construction of angle of measure 120° (ii)].

Step 2: With C as center, draw an arc of convenient radius in the interior of ∠CAD.

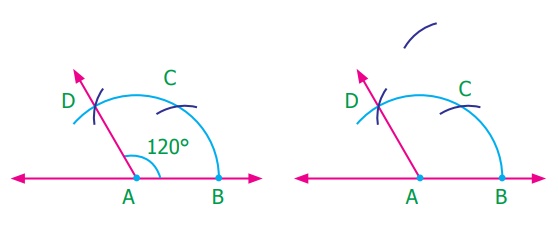
Step 3: With the same radius and D as center, draw an arc to cut drawn in step 3 at E.

Step 4: Join AE. Then ∠BAD = 90° is the required angle