Exercise 5.2 (Angles formed by a transversal)

Exercise 5.2

1. From the figures name the marked pair of angles.

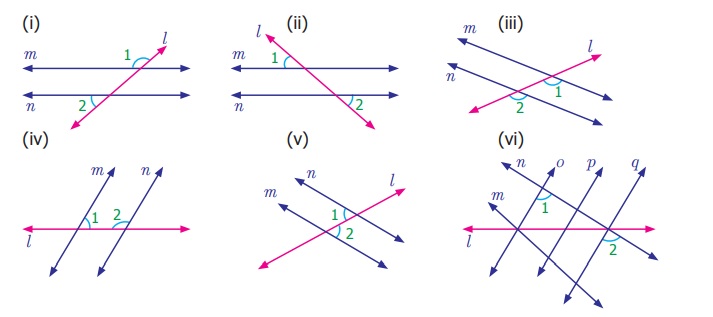
Answer:

(i)  The marked angles are exterior angles on the same side of the transversal

(ii) The angles are alternate exterior angles

(iii) The angles are corresponding angles

(iv) The angles are interior angles on the same side of the transversal

(v) The angles are alternate interior angles. 

(vi) The angles are corresponding angles.

2. Find the measure of angle x in each the following figures.

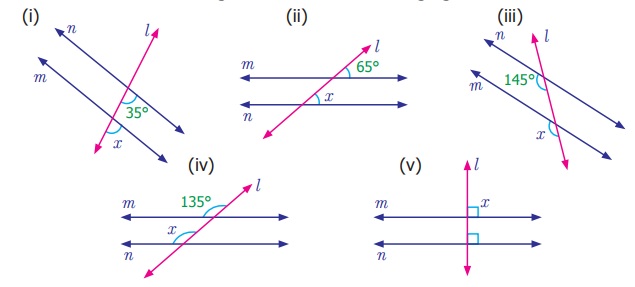
Answer:

(i) x = 35° (corresponding angles)

(ii) x = 65° (corresponding angles)

(iii) x = 145° (corresponding angles)

(iv) x = 135° (corresponding angles)

(v) x = 90° (perpendicular angles) 

3. Find the measure of angle y in each the following figures.

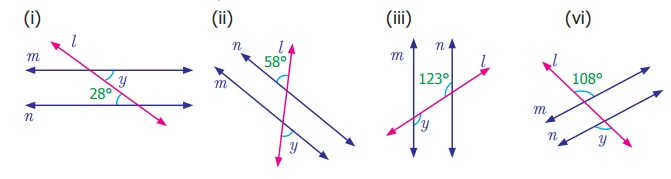
Answer:

(i) y = 28° (alternate angles)

(ii) y = 58° (alternate exterior angles)

(iii) y = 123° (alternate angles)

(iv) y = 108° (alternate exterior angles)

4. Find the measure of angle z in each the following figures.

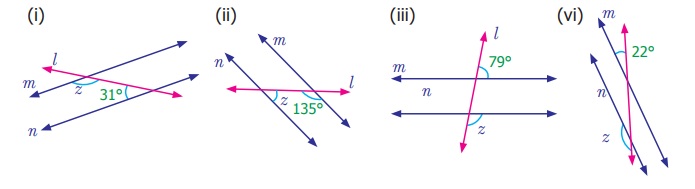
Answer:

(i) z + 31° = 180° (interior angles)

z = 180° – 31° = 149°

(ii) z + 135° = 180° (interior angles)

z = 180° – 35° = 45° 

(iii) z + 79^o = 180° (exterior angles)

z = 180° – 79° = 101°

(iv) z + 22° = 180° (exterior angles)

z = 180° – 22° = 158°

5. Find the value of angle a in each the following figures.

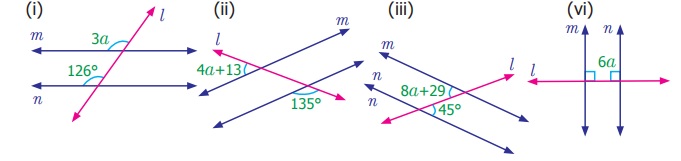
Answer:

(i) 3a = 126° (corresponding angles)

a = 42°

(ii) 4a + 13 + 135° = 180° (exterior angles)

4a + 148° = 180°

4a = 180°– 148° = 32°

a = 8°

(iii) 8a + 29 = 45° (alternate angles)

8a = 45° – 29° = 16°

a = 2°

(iv) 6a = 90° (right angle)

a = 15° 

6. Find the value of angle x in both the figures.

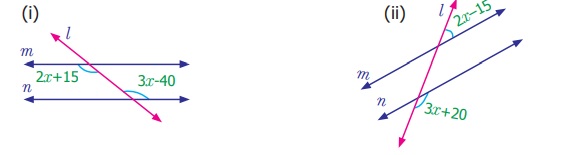
Answer:

(i) 2x + 15 = 3x – 40

(alternate interior angles)

3x – 2x = 15 + 40

x = 55°

(ii) 2x – 15 + 3x + 20 = 180°

(exterior angles)

5x + 5 = 180°

5x = 180° – 5° = 175°

x = 35°

7. Anbu has marked the angles as shown below in (i) and (ii). Check whether both of them are correct. Give reasons.

Answer:

(i) No since interior angles on the same side of the transversal are supplementary.

(ii) No corresponding angles are equal.

8. Mention two real-life situations where we use parallel lines.

Answer: 

Railway Track and front bar in the window.

9. Two parallel lines are intersected by a transvesal. What is the minimum number of angles you need to know to find the remaining angles. Give reasons.

Answer: 

Minimum number of angles is 1. Using the concept of linear pair of angles, we can find one more angle and by the concepts of corresponding angle and by the concepts of corresponding angles and alternate angles (interior and exterior) we would find all other angles.

Objective type questions

10. A line which intersects two or more lines in different points is known as

(i) parallel lines

(ii) transversal

(iii) non-parallel lines

(iv) intersecting line

Answer : (ii) transversal

11. In the given figure, angles a and b are

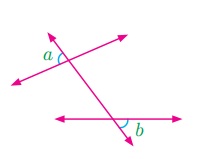
(i) alternate exterior angles

(ii) corresponding angles

(iii) alternate interior angles

(iv) vertically opposite angles

Answer : (i) alternate exterior angles

12. Which of the following statements is ALWAYS TRUE when parallel lines are cut by a transversal

(i) corresponding angles supplementary.

(ii) alternate interior angles supplementary.

(iii) alternate exterior angles supplementary.

(iv) interior angles on the same side of the transversal are supplementary.

Answer : (iv) interior angles on the same side of the transversal are supplementary.

13. In the diagram, what is the value of angle x?

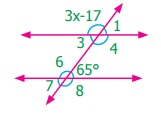
(i) 43°

(ii) 44°

(iii) 132°

(iv) 134°

Answer : (ii) 44°

ANSWERS

Exercise 5.2

1. (i) The angles are exterior angles on the same side of the transversal

(ii) The angles are alternate exterior angles

(iii) The angles are corresponding angles

(iv) The angles are interior angles on the same side of the transversal

(v) The angles are alternate interior angles

(vi) The angles are corresponding angles

2. (i) 35° (ii) 65° (iii) 145° (iv) 135° (v)90°

3. (i) 28° (ii) 58° (iii) 123° (iv) 108°

4. (i) 149° (ii) 45° (iii) 101° (iv) 158°

5. (i) 42° (ii) 8° (iii) 2° (iv) 15°

6. (i) 55° (ii) 35°

7. (i) No. Since, interior angles on the same side of the transversal are supplementary.

(ii) No. Since Corresponding angles are equal.

9. Minimum number of angles is 1. Using the concept of linear pair of angles, we can find one more angle and by the concepts of corresponding angles and alternate angles (interior and exterior) we could find all other angles.

Objective type questions

10. (ii) transversal

11. (i) alternate exterior angle

12. (iv) interior angles on the same side of the transversal are supplementary

13. (ii) 44°