Asymmetric Key Cryptography

Asymmetric-Key Cryptography

An asymmetric-key (or public-key) cipher uses two keys: one private and one public. We discuss two algorithms: RSA and Diffie-Hellman.

RSA

The most common public key algorithm is RSA, named for its inventors Rivest, Shamir, and Adleman (RSA). It uses two numbers, e and d, as the public and private keys.

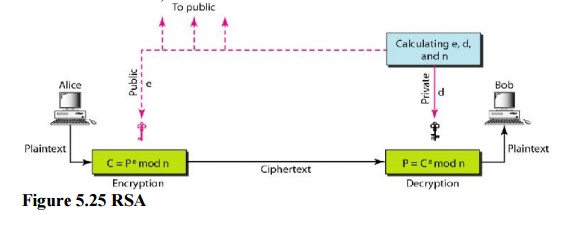
Encryption

Anyone who needs to send a message to Bob can use name e. For example, if Alice needs to send a message to Bob, she can change the message, usually a short one, to an integer. This is the plaintext. She then calculates the ciphertext, using e and n.

C=pe(mod n) Alice sends C, the ciphertext, to Bob.

Decryption

Bob keeps Ф and d private. When he receives the ciphertext, he uses his private key d to decrypt the message:

P= Cd(mod n)

Restriction

For RSA to work the value of P must be less than the value of n. If P is a large number, the plaintext needs to be divided into blocks to make P less than n.

Applications

Although RSA can be used to encrypt and decrypt actual messages, it is very slow if the message is long. RSA, therefore, is useful for short messages such as a small message digest or a symmetric key to be used for a symmetric-key cryptosystem. In particular, we will see that RSA is used in digital signatures and other cryptosystems that often need to encrypt a small message without having access to a symmetric key.RSA is also used for authentication.

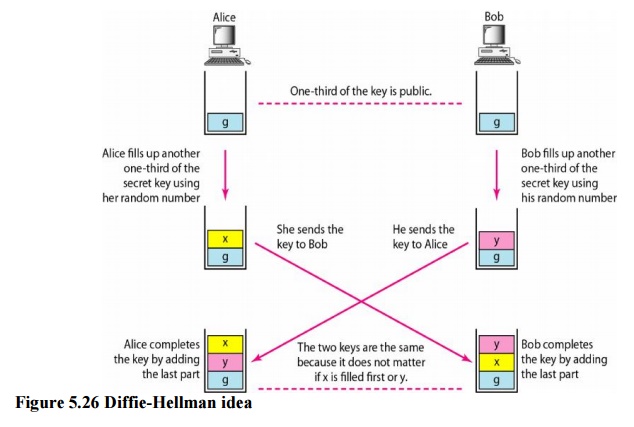
Diffie-Hellman

RSA is a public-key cryptosystem that is often used to encrypt and decrypt symmetric keys. Diffie-Hellman, on the other hand, was originally designed for key exchange. In the Diffie-Hellman cryptosystem, two parties create a symmetric session key to exchange data withouthaving to remember or store the key for future use. They do not have to meet to agree on the key; it can be done through the Internet.