Algebra

Chapter 3

ALGEBRA

Learning objectives

● To identify variables and constants in the given terms of an algebraic expression.

● To find the coefficients of the terms of an algebraic expression.

● To identify like and unlike terms.

● To add and subtract algebraic expressions with integer co-efficients.

● To form simple expressions in two variables.

● To understand simple linear equations and solve problems.

Recap

In class VI, we have learnt how geometric patterns and number patterns can be generalised using variables and constants. A variable takes different values which is represented by x,y,z... and constant has numerical values such as 31, − 7, 3/10 etc.

For example,

(i) The number of Ice − candy sticks required to form one square () is four sticks, for two squares is eight sticks, for three squares is twelve sticks and so on.

Continuing in the same way, it is clear that if the number of squares () to be formed is k (any natural number), then the number of candy sticks required will be 4 × k = 4k, where k is a variable and 4 is a constant.

This can be observed in the following table:

(ii) Observe the following pattern

7×9 = 9×7,

23×56 = 56×23,

999 × 888 = 888 × 999

This can be generalised as a × b = b × a, where a, b are variables.

Try these

1. Identify the variables and constants among the following terms:

a,11 − 3x, xy, − 89, − m, − n, 5, 5ab, − 5, 3y , 8pqr, 18, − 9t, − 1,− 8

Variables : a, –3x, xy, –m, n, 5ab, 3y, 8 pqr, –9t

Constants : 11, –89, 5, –5, 18,–1, –8

2. Complete the following table:

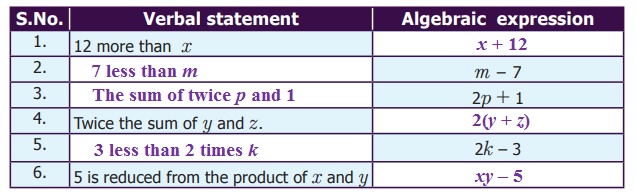
Note : Algebraic statements are also known as Algebraic expressions.

Introduction

Consider the situation. Murugan’s mother gave him ₹100 to buy 1 kilogram of sugar. If the shopkeeper returned ₹58, what is the price of sugar?

Let us see another situation. Jayashri wants to share chocolates among her friends on her birthday. She had ₹190 in her piggy bank. If she could buy 95 chocolates with that amount, then what is the price of one chocolate?

Did you get the answers? How did you work out?

You might have created numeric equations like 100 – 58 = ? and 190 ÷ 95 = ? and then solved it. Isn’t it? In both the cases, question mark (?) stands for an unknown value. Instead of using question marks everytime, we could use the letters like x, y, a, b …

Let us learn more about this interesting branch of mathematics which deals with the methods of finding the unknown values.

MATHEMATICS ALIVE - ALGEBRA IN REAL LIFE