Terms and Co-efficients

Terms and Co-efficients

We combine variables and constants using the mathematical operations addition and subtraction to construct algebraic expressions.

For example, the expression 6x + 1 is obtained by adding two parts 6x and 1. Here 6x and 1 are known as terms. The term 6x is a variable and the term 1 is a constant, since it is not multiplied by a variable. Also we say that 6, x are the factors of the term 6x.

Similarly, in the expression 3ab + 5c, the terms are 3ab and 5c. The factors of the term 3ab are 3, a and b. In the same way, the factors of the term 5c are 5 and c.

Now let us further try to understand the terms of an algebraic expression.

Observe the Fig.3.2

What is the perimeter of the given figure?

The perimeter, 'P' = x + 5 + 6 + y + 5 + 4 + z + w units,

= x + y + z + w + (5 + 6 + 5 + 4)

= x + y + z + w + 20,

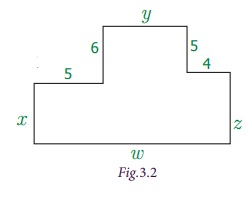
where x, y, z, w are variables and 20 is a constant.

Note that, in the above expression, 5 terms are combined by using addition.

Consider another example as 6x − 5y + 3. To find the terms of the expression, we write 6x + (−5y)+3. Here the terms are 6x, (−5y) and 3. An expression may have one, two, three or more terms.

Also, a term may be any one of the following:

i) a constant such as 8, −11, 7, −1,…

ii) a variable such as x,a,p,y,…

iii) a product of two or more variables such as xy, pq, abc, ...

iv) a product of constant and a variable/variables such as 5x, −7pq, 3abc,…

Think

Can we use the operations multiplication and division to combine terms?

Note

An algebraic expression can have one term, two terms or more than two terms. An expression with one term is called a monomial, two terms is called a binomial and three terms is called a trinomial. An expression with one or more terms is called a polynomial. For example, the expression 2x is a monomial, 2x + 3y is a binomial, and 2x + 3y + 4z is a trinomial. All the expressions given above are polynomials.

Activity

To further strengthen the understanding of variables and constants, let us do the following activity.

Consider, two baskets of cards. One containing constants and the other containing variables. Pick a constant from the first basket and a variable from the second basket and form a variable term by expressing it as a product. Write all the possible terms that can be constructed using the given constants and variables.

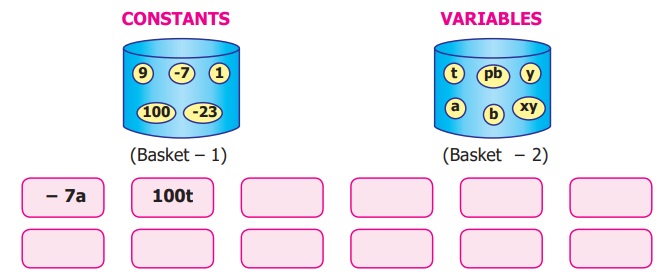
Answer: 

Try this

Complete the following table by forming expressions using the terms given. One is done for you.

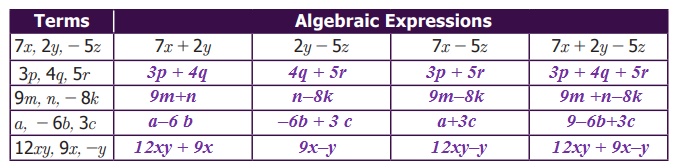
Example 3.1

Identify the variables, terms and number of terms in each of the following expressions: (i) 12 − x (ii) 7 + 2y (iii) 29+3x+5y (iv) 3x–5+7z

Solution

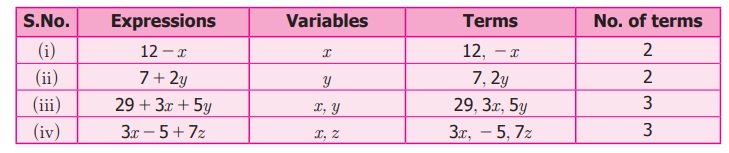
1. Co-efficient of a term

A term of an algebraic expression is a product of factors. Here each factor or product of factors is called the co-efficient of the remaining product of factors.

For example, in the term 5xy, 5 is the co-efficient of remaining factor product xy. Similarly x is the co-efficient of 5y; 5x is the co- efficient of y. The constant 5 is called the numerical co-efficient, and others are called simply co-efficients.

A co-efficient can either be a numerical factor or an algebraic factor or product of both.

Since we often talk about the numerical co -efficients of a term, if we say “co-efficient”, it will be understood that we are referring to the numerical co-efficient. If no numerical co-efficient appears in a term, then the co-efficient is understood to be 1.

Consider the term − 6ab. It is the product of three factors −6, a and b . Also it can be written as a product of two factors such as −6a × b, −6b × a and −6 × ab.

The co-efficient of ‘a’ is −6b

The co-efficient of ‘b’ is −6a

The co-efficient of ‘ab’ is – 6

Thus −6 is the numerical co-efficient of the term −6ab.

Example 3.2

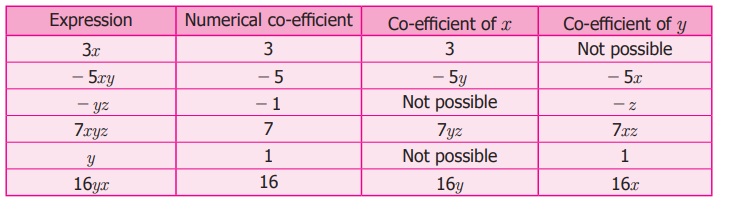
Find the numerical co-efficient of the following terms. Also, find the co efficient of x and y in each of the term: 3x, −5xy, −yz, 7xyz, y, 16yx.

Solution