Exercise 3.4

Exercise 3.4

Miscellaneous Practice problems

1. Subtract −3ab −8 from 3ab + 8. Also, subtract 3ab + 8 from −3ab −8.

Subtract –3 ab –8 from 3 ab + 8

3ab + 8 – (–3 ab – 8)

3ab + 8 + 3 ab + 8

3ab + 3 ab + 8 + 8

(3 + 3) ab +16

6 ab + 16

Subtract 3ab + 8 from –3ab –8

–3ab – 8 – (3 ab + 8)

– 3ab –8 – 3 ab – 8

– 3ab – 3 ab – 8 – 8

(–3 –3) ab –16

– 6 ab –16

2. Find the perimeter of a triangle whose sides are x + 3y, 2x + y, x − y.

Sides of the triangle a = x + 3y

                               b = 2x + y

                               c = x – y

Perimeter of a triangle = a + b + c

                                   = x + 3y + 2x + y + x – y

                                   = x + 2x + x + 3y + y – y

                                 = (l +2 + l)x + (3 + l– l) y

                                 = 4x + 3y

3. Thrice a number when increased by 5 gives 44. Find the number.

Thrice a number when increased by 5 gives 44.

Let the number be x

3x + 5 = 44

3x + 5 – 5 = 44 – 5

 3x = 39

 3/3 x = 39/3

 x = 13

The number x =13

4. How much smaller is 2ab + 4b − c than 5ab − 3b + 2c

5ab – 3b + 2c – (2ab + 4b – c)

5ab – 3b + 2c – 2ab – 4b + c

5ab – 2ab – 3b – 4b + 2c + c

(5–2) ab + (– 3 – 4)b + (2+l) c

3ab – 7b + 3c

5. Six times a number subtracted from 40 gives −8. Find the number.

Six times a number subtracted from 40 gives –8

Let the number be x

40 – 6x = –8

40 – 40 – 6x = –8 – 40

 – 6x = –48

–6x / –6 = –48 / –6

 x = 8

The number x = 8

Challenge Problems

6. From the sum of 5x + 7y − 12 and 3x − 5y + 2, subtract the sum of 2x − 7y − 1 and −6x + 3y + 9.

The sum 5x + 7y –12 + 3x – 5y + 2

5x + 3x + 7y –5y –12 + 2

(5 + 3)x + (7 – 5) y –10

8x + 2y – 10

The sum 2x – 7y –1 – 6x + 3y + 9

2x – 6x –7y + 3y –1 + 9

(2 – 6)x + (–7 +3)y +8

 – 4x – 4y + 8

(8x + 2y –10) – (–4x – 4y + 8)

8x + 2y – 10 + 4x + 4y – 8

8x + 4x + 2y + 4y – 10 – 8

(8 + 4)x + (2 + 4)y – 18

12x + 6y –18

7. Find the expression to be added with 5a − 3b + 2c to get a − 4b − 2c?

a – 4b – 2c – (5a –3b + 2c)

a – 4b –2c –5a +3b –2c

a – 5a – 4b + 3b – 2c – 2c

(l – 5)a + (–4 +3)b + (–2 –2)c

– 4a – b – 4c

– 4a – b – 4c to be added with 5a – 3b + 2c to get a – 4b – 2c

8. What should be subtracted from 2m + 8n + 10 to get −3m + 7n + 16?

2m + 8n + 10 – (–3m + 7n + 16)

2m + 8n + 10 + 3m – 7n – 16

2m + 3m + 8n – 7n + 10 –16

(2+3) m + (8 – 7) n – 6

5m + n – 6

5m + n – 6 should be subtracted from

2m + 8n + 10 to get –3m + 7n + 16 

9. Give an algebraic equation for the following statement:

“ The difference between the area and perimeter of a rectangle is 20”

Area of a rectangle = lb

Perimeter of a rectangle = 2(l+b)

The different between the area and Perimeter of a rectangle is 20.

 lb – 2 (l + b) = 20

10. Add: 2a + b + 3c and a + 1/3 b + 2/5 c

2a + b + 3c + (a + 1/3 b + 2/5 c)

2a + a + b + 1/3 b + 3c + 2/5 c

(2+1) a + (1 + 1/3) b + (3 + 2/5) c

3a + 4/3 b + 17/5 c

Puzzles are instrumental for the origin of Algebra. Leelavathi is the first puzzle book in India written by Baskaracharya (Baskara II) who lived in Maharashtra during 12th century. The modified version of the interesting puzzle is for you.

“The beads from a pearl necklace fell down. One third of the pearls fell on the ground. One fifth of the pearls rolled under cot. Two persons started collecting the pearls. One person was able to collect one sixth and the other person collected one tenth of the pearls. If only 6 pearls are left in the necklace, find the total number of pearls in the necklace?”

Let the total number of pearls be x.

Using the given details, we can create an equation.

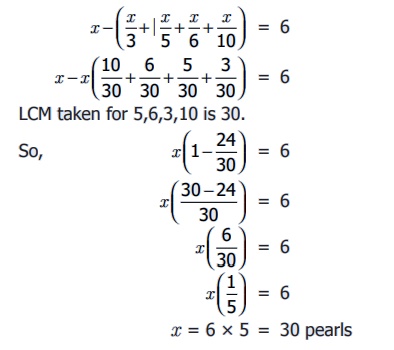
x = 6 × 5 = 30 pearls

ANSWERS

EXERCISE-3.4

1. 6 ab + 16; − 6ab − 16

2. 4 x + 3y

3. x = 13

4. 3ab − 7b + 3c

5. x = 8

 Challenge Problems

6. 12x + 6 y − 18

7. −4a − b − 4c

8. 5m + n − 6

9. lb − 2 ( l + b) = 20

10. 3a + 4/3 b + 17/5 c