Simple linear equations

Simple linear equations

Now, let us learn to construct simple linear equations and solve them.

1. Construction of linear equations

Consider an expression 7x + 3, where x is the variable.

When x = 2, the value of the expression is (7 × 2) + 3 = 14 + 3 = 17.

Also, this can be written as 7x + 3 = 17, when x = 2. 7x + 3 = 17 is called an equation.

Moreover, no value of x other than 2 satisfies the condition 7x + 3 = 17. Thus x = 2 is called the solution to the equation 7x + 3 = 17.

An equation, is always equated to either a numerical value or another algebraic expression. The equality sign shows that the value of the expression to the left of the ‘=’ sign is equal to the value of the expression to the right of the ‘=’ sign. In the above example, the expression 7x + 3 on the left side is equal to the constant 17 on the right side.

In general, the RHS of an equation is just a number. But, this need not be always be so. The RHS may be an expression containing the variable. For example, the equation 7x + 3 = 3x − 1 has the expression 7x + 3 on the left and 3x − 1 on the right separated by an equality sign.

Let us look at some situations where we have the value of an expression without actually knowing the values of each of the variables.

The price of 10 chairs and 4 tables is ₹ 4000. We are not given the price of a chair or a table. Let us take the price of one chair as ₹ x and one table as ₹ y. Then the cost of 10 chairs and 4 tables is 10x + 4y. Therefore, 10x + 4y = 4000. This is an equation in two variables x and y taking the value 4000. Let us consider some more examples and find the algebraic equations.

1. “The cost of an apple and 2 mangoes is ₹ 120”

If the price of an apple is a and one mango is m, then the required equation is a + 2m = 120.

2. “A rectangle of some dimensions has perimeter 50 cm”.

If l and b are the length and breadth of the rectangle then we write 2 (l + b) = 50.

3. “Thamarai is 4 years elder to her sister Selvi and their ages add upto 24”

The ages of Thamarai and her sister are treated as variables. Although, their ages are different, we consider this as one variable, because the age of Thamarai is associated to the age of Selvi.

Suppose, if Selvi’s age is 10, then the age of Thamarai is 10 + 4 = 14. In the same way, if the age of Selvi is x, then the age of Thamarai is x + 4.

Thus we can form an equation as x + (x + 4) = 24. Otherwise, 2x + 4 = 24.

Hence an equation can be looked as algebraic expression equated to either a constant or any other algebraic expression.

Try these

Try to construct algebraic equations for the following verbal statements.

1. One third of a number plus 6 is 10

1/3 x + 6 = 10

2. The sum of five times of x and 3 is 28.

5x + 3 = 28

3. Taking away 8 from y gives 11.

y – 8 = 11

4. Perimeter of a square with side a is 16cm.

4a =16

5. Venkat’s mother’s age is 7 years more than 3 times Venkat’s age. His mother’s age is 43 years.

Let Venkat’s age is x

Venkat’s mother's age = 3x + 7

3x + 7 = 43

2. Solving an equation

An equation is like a weighing balance with equal weights on both of its pans, in which case the arm of the balance are exactly horizontal.

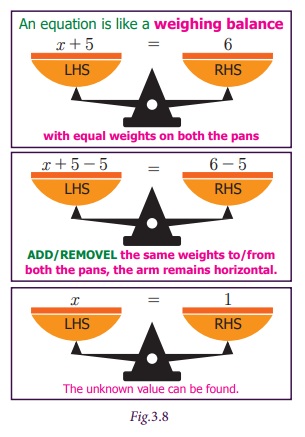
If we add the same weights to both the pans, the arms remains horizontal. In the same way, if we remove the same weights from both the pans, then also the arm remains horizontal. We use the same principle for solving an equation.

We use the following principles to separate the variables and constants thereby solving an equation.

1. If we add or subtract the same number on both sides of the equation, the value remains the same. For example, to solve x + 5 = 12, we have to subtract 5 on both sides, for separating the constants and variables of the equation, that is x + 5 − 5 = 12 − 5.

x + 0 = 7 Hence x = 7 [since 0 is the additive identity]

Think

Why should we subtract 5 and not some other number? Why don’t we add 5 on both sides? Discuss.

2. Similarly, if we multiply or divide the equation with the same number on both sides, the equation remains the same. For example, to solve the equation 5y = 20, divide by 5 on both sides.

Thus we have 1/5 × = 5y = 20/5 . Therefore, y = 4

3. An equation remains the same, when the expressions on the left and on the right are interchanged. The equation 7x + 3 = 17 is the same as 17 = 7x + 3. Similarly, the equation 7x + 3 = 3x − 1 is the same as 3x −1 = 7x + 3.

Try this

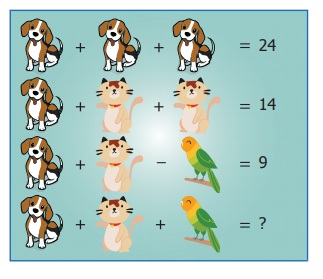
If the dogs, cats and parrots represent unknowns, find them. Substitute each of the values so obtained in the equations and verify the answers.

8 + 8 + 8 = 24

8 + 3 + 3 = 14

8 + 3 – 2 = 9

8 + 3 + 2 = 13

Example 3.11 Find two consecutive natural numbers whose sum is 75.

Solution

The numbers are natural and consecutive. Let the numbers be x and x + 1.

Given that,

x+ (x + 1) = 75

2x + 1 = 75

2x + 1 –  1 = 75 − 1 [Subtract 1 on both sides]

2x + 0 = 74

 2x/2 = 74/2 [Divide 2 at both sides]

x = 37 and x + 1 = 38

Therefore, the required numbers are 37 and 38.

Example 3.12

A person has ₹ 960 in denominations of ₹ 1, ₹ 5 and ₹ 10 notes. The number of notes in each denomination is equal. What is the total number of notes?

Solution

Let the number of notes in each denomination be x.

Then x + 5x + 10x = 960

(1 + 5 + 10)x = 960

16x = 960

Divide by 16 on both the sides,

16x/16 = 960/16 = 60

Therefore, x = 60

Thus, the number of notes in each denomination is 60.

Example 3.13

In an examination, a student scores 4 marks for every correct answer and loses one mark for every wrong answer. If he answers 60 questions in all and gets 130 marks, find the number of questions he answered correctly.

Solution

Let the number of correct answers be x

Thus the number of wrong answers = 60 – x

Then, 4x − 1 (60 − x) = 130

4x − 60 + x = 130

4x + x − 60 + 60 = 130 + 60 [Add 60 on both sides]

5x + 0 = 190

5x = 190

Divide by 5 on both the sides,

 5x/5 = 190/5 = 38

 x = 38

Hence, the number of correct answer is 38.

Example 3.14

A school bus starts with full strength of 60 students. It drops some students at the first bus stop. At the second bus stop, twice the number of students get down from the bus. 6 students get down at the third bus stop and the number of students remaining in the bus is only 3. How many students got down at the first stop?

Solution

Since we do not know the number of students who get down at the first stop, let us take the number as x. The number of students get down at the second bus stop is 2x.

x+ 2x +6+3 = 60

(1 + 2) x + 9 = 60

3x + 9 =60

3x + 9 – 9 = 60 − 9 [Subtract 9 on both sides]

3x = 51

3x / 3 = 51/3  [Divide by 3 on both sides]

Therefore, x = 17

Thus, the number of students got down in the first bus stop is 17.

Example 3.15

A cricket team won two matches more than they lost. If they win they get 5 points and for loss − 3 points, how many matches have they played if their total score is 50.

Solution

Let the number of matches lost = x

Then number of matches won = x + 2

Given that, 5(x + 2) + ( − 3)x= 50

5x + 10 − 3x = 50

2x + 10 = 50

2x + 10 – 10 = 50− 10   (Subtract 10 on both sides)

2x = 40

Divide by 2 on both the sides, x = 20

Therefore, the number of matches played is x + x + 2 = 2x + 2

 = (2×20)+2

= 40 + 2

= 42.

Try this

Kandhan and Kavya are friends. Both of them are having some pens.

Kandhan : If you give me one pen, then we will have equal number of pens. Will you?

Kavya : But, if you give me one of your pens, then mine will become twice as yours. Will you?

Construct algebraic equations for this situation. Can you guess and find the actual number of pens, they have?

Let Kandhan has x pens

Kavya has y pens

If Kavya gives 1 pen to Kandhan both will have equal number of pens

x + 1 = y – 1

x – y = – l – l

x – y = – 2 ………… (1)

If Kandhan gives 1 pen to Kavya, Kavya will become twice as Kandhan.

y + l = 2(x – 1)

y + 1 = 2x – 2

2x – y = 1 + 2 = 3

         2x – y = 3 …………. (2)

         2x – y = 3

           x – y = –2

Subtract –  +      +

                  x = 5

Substitute x = 5in (1)

x – y = –2

5 – y = –2

–y = –2 –5 = –7

y =7

Kandhan has 5 pens

Kavya has 7 pens