Addition and Subtraction of Algebraic expressions

Addition and Subtraction of Algebraic expressions

We have discussed about algebraic expressions. Now, let us see how to add and subtract algebraic expressions.

Situation: Kannan has some number of beads and Aravind has 20 beads more than Kannan. Kavitha says that she has 3 more beads than the number of beads that Kannan and Aravind together have. How will you find the number of beads that Kavitha have.

Now we see that even though 3 persons are involved with 3 unknown quantities, we make use of one variable, since all the three variables are related.

Let that one variable be x which represents the number of beads that Kannan has.

Aravind has 20 more beads than Kannan. That is x + 20.

Kavitha has 3 beads more than Kannan and Aravind have together. So, the number of beads that Kavitha has is given by x+x+20+3.

Now, we change the situation. Instead of Aravind has 20 more beads than Kannan, suppose Aravind has 20 beads less than Kannan.

If Kavitha has 3 beads more than what Kannan and Aravind have together, then find the number of beads that Kavitha has.

Now, Aravind has x – 20 beads. So, the number of beads that Kavitha has, is given by x + x – 20 + 3.

For example, to add 8ab, 4ab and 2ab, where ab is variable, we add the co-efficients alone, that is 8ab + 4ab + 2ab = (8 + 4 + 2) ab = 14 ab = 14ab.

In the same way, we can add the algebraic expressions. Let us try to add the expressions 11y + 7 and 5y − 3, where 11y and 5y are like terms with a variable y and 7 and −3 are

Hence, (11y + 7) + (5y − 3) = [11y + 5y] + [7 + ( − 3)]

 = [(11 + 5) y] + (7 − 3)]

 = 16y + 4.

Try this

Add the terms: 

i) 3p, 14p

3p + 14p = 17p

ii) m, 12m, 21m

m + 12m + 21m = 34m

iii) 11abc, 5abc

11 abc + 5 abc = 16 abc

iv) 12y, −y

12y + –y = 11y

v) 4x, 2x, − 7x

4x + 2x + – 7x

6x – 7x = –x 

Example 3.5

Add the expressions: (i) pq −1 and 3pq + 2 (ii) 8x + 3 and 1 − 7x

Solution

(i) (pq − 1) + (3pq + 2) = (pq + 3pq) + ( − 1 + 2)

 = (1 + 3)pq + 1

= 4pq + 1

(ii) (8x + 3) + (1 − 7x) = 8x + 3 + 1 − 7x

 = (8x − 7x) + (3 + 1)

 = (8 − 7) x + 4

 = x + 4.

Subtraction of a term can be looked as addition of its additive inverse as we saw in subtraction of integers. To understand subtraction of algebraic expression, let us consider subtraction of algebraic expression with one term.

For example, to subtract 6y from 12y, we can add 12y and (− 6y).

Thus we have, 12y + ( − 6y) = 12y − 6y

= (12 − 6)y = 6y.

Now, let us subtract – mn from 3mn. Additive inverse of – mn is mn. Hence, we have to add mn with 3mn. Thus, 3mn + mn = (3 + 1)mn = 4mn.

Similarly, we can subtract two algebraic expressions. For example, to subtract 13a − 2 from 25a + 11, we have to add the additive inverse of 13a – 2 with 25a + 11.

Additive inverse of 13a–2 is −(13a−2) = −13a + 2

Therefore, 25a + 11 − (13a – 2) = (25a + 11) + (−13a +2)

  = (25a + 11) + (−13a +2)

 = (25a − 13a) + (11 + 2)

 = 12a + 13

Note

1. Subtracting 4y is the same as adding – 4y and subtracting – 11x is the same as adding 11x.

2. We know that, – 3 is the additive inverse of 3. In the same way – x is an additive inverse of x. Hence, x, – x are equal in numerical value; but opposite in sign.

Therefore, x+(–x) = 0. But, x – (–x) = x+x = 2x.

Example 3.6

Subtract: i) 7pq from 11pq ii) – a from a iii) 5x + 7 from 21x + 9

Solution

(i) 11pq – 7pq. Additive inverse of 7pq is − 7pq

 11pq + ( − 7pq) = 11pq − 7pq = (11 − 7)pq = 4pq

(ii) a – (–a). Additive inverse of −a is a.

So, a + a = 2a

(iii) 21x + 9 – (5x + 7). Additive inverse of 5x + 7 is – (5x + 7).

(21x + 9) + [– (5x + 7)] = (21x + 9) – (5x + 7)

 = 21x + 9 − 5x – 7

 = (21 − 5)x + (9 − 7)

 = 16x + 2.

Think

3x + (y − x) = 3x + y − x. But, 3x − (y − x) ≠ 3x − y − x. Why?.

Example 3.7

Simplify:100x + 99y – 98z + 10x + 10y + 10z – x – y + z

Solution

In the given algebraic expression, x,y,z are the variables.

Let us group the like terms.

100x + 99y − 98z + 10x + 10y + 10z − x − y + z

 = (100x + 10x − x) + (99y + 10y − y) + ( −98z + 10z + z)

 = (100 + 10 − 1)x + (99 + 10 − 1)y + ( −98 + 10 + 1)z

 = (110 − 1)x + (109 − 1)y + ( −98 + 11)z

 = 109x + 108y + ( −87)z

 = 109x + 108y − 87z.

Note

For adding or subtracting algebraic expressions, we can write the like terms one after the other horizontally by using brackets or one below the other vertically.

Example 3.8

i) Add: 3x − 4y + z and 2x − z + 3y ii) Subtract 2x − 5y from 4x + 3y

Solution

(i) (3x − 4y + z) + (2x − z + 3y)

 = (3x + 2x) + ( −4y + 3y) + (z − z)

 = (3 + 2)x + ( −4 + 3)y + (1 − 1)z

 = 5x − 1y + 0z

 = 5x − y.

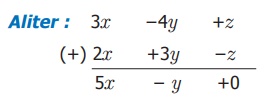
(i) (4x + 3y) − (2x − 5y)

 = (4x + 3y) + ( −2x + 5y)

 = (4x − 2x) + (3y + 5y)

 = (4 − 2)x + (3 + 5)y

 = 2x + 8y.

Think

What will you get if twice a number is subtracted from thrice the same number?

Example 3.9

Mani and his friend Mohamed went to a hotel for dinner. Mani had 2 idlies and 2 dosas whereas Mohamed had 4 idlies and 1 dosa. If the price of each idly and dosa is x and y respectively, then find the bill amount in x and y.

Solution

Given that, the price of one idly is ‘x’ rupees and the price of one dosa is ‘y’ rupees

So, Mani’s bill amount: (2 × x) + (2 × y) = (2x + 2y)

Mohamed’s bill amount: (4 × x) + (1 × y) = 4x + y

Therefore, the total bill amount = (2x + 2y) + (4x + y)

 = (2 + 4)x + (2 + 1)y = 6x + 3y.

Aliter:

In total, they had 2 + 4 = 6 idlies. i.e. 6 × x = 6x

and 2 + 1 = 3 dosas. i.e. 3 × y = 3y

Therefore, the total bill amount = 6x + 3y.

Example 3.10

Rani earns ₹ 200 on the first day and spends some amount in the evening. She earns ₹ 300 on the second day and spends double the amount as she spents on the first day. She earns ₹ 400 on the third day and spends 4 times the amount as she spents on the first day. Can you give an algebraic expression of the total amount with her, at the end of the third day.

Solution

The amount earned on the first day is ₹ 200.

Let the amount spent on the first day be ₹ x. Amount with her at the end of the first day is (200 − x).

Amount earned on the second day is ₹ 300 and the amount spent on the second day is ₹ 2x. The amount left on the second day is 300 − 2x.

Similarly, the net amount that she would have on the third day is 400 − 4x. Therefore, the total amount that she would have at the end of three days is (200 − x) + (300 − 2x) + (400 − 4x).

That is, 200 + 300 + 400 + ( − 1 − 2 − 4)x

 = 900 + ( −7)x

Thus the required algebraic expression is 900 − 7x.

Activity

Here is a magic number trick that you can perform using Algebra.

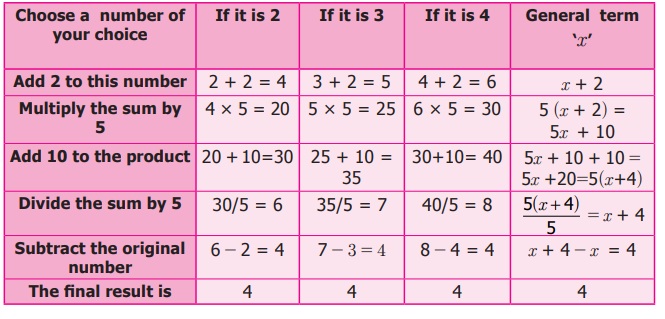
Everyone will end up with the same result 4 irrespective of the number they think. Play this number game with your friends and surprise them. We generalized the pattern in the final column using algebraic expressions. Observe the same and create your own number game and verify whether it works for any number by finding the general term.