Selected LP Applications: Blending and Refining

SELECTED LP APPLICATIONS

This section presents realistic LP models in which the definition of the variables and the construction of the objective function and constraints are not as straight-forward as in the case of the two-variable model. The areas covered by these appli-cations include the following:

1. Urban planning.

2. Currency arbitrage.

3. Investment.

4. Production planning and inventory control.

5. Blending and oil refining.

6. Manpower planning.

Each model is fully developed and its optimum solution is analyzed and interpreted.

5. Blending and Refining

A number of LP applications deal with blending different input materials to produce products that meet certain specifications while minimizing cost or maximizing profit. The input materials could be ores, metal scraps, chemicals, or crude oils and the output products could be metal ingots, paints, or gasoline of various grades. This section pre-sents a (simplified) model for oil refining. The process starts with distilling crude oil to produce intermediate gasoline stocks and then blending these stocks to produce final gasolines. The final products must satisfy certain quality specifications (such as octane rating). In addition, distillation capacities and demand limits can directly affect the level of production of the different grades of gasoline. One goal of the modeLis deter-mine the optimal mix of final products that will maximize an appropriate profit func-tion. In some cases, the goal may be to minimize a cost function.

Example 2.3-7                  (Crude Oil Refining and Gasoline Blending)

Shale Oil, located on the island of Aruba, has a capacity of 1,500,000 bbl of crude oil per day. The final products from the refinery include three types of unleaded gasoline with different octane numbers (ON): regular with ON = 87, premium with ON = 89, and super with ON = 92. The refining process encompasses three stages: (1) a distillation tower that produces feedstock (ON = 82) at the rate of .2 bbl per bbl of crude oil, (2) a cracker unit that produces gasoline stock (ON = 98) by using a portion of the feedstock produced from the distillation tower at the rate of .5 bbl per bbl of feedstock, and (3) a blender unit that blends the gasoline stock from the cracker unit and the feedstock from the distillation tower. The company estimates the net profit per barrel of the three types of gasoline to be $6.70, $7.20, and $8.10, respectively. The input capacity of the cracker unit is 200,000 barrels of feedstock a day. The demand limits for regular, premium, and super gasoline are 50,000,30,000, and 40,000 barrels per day. Develop a model for determining the optimum production schedule for the refinery.

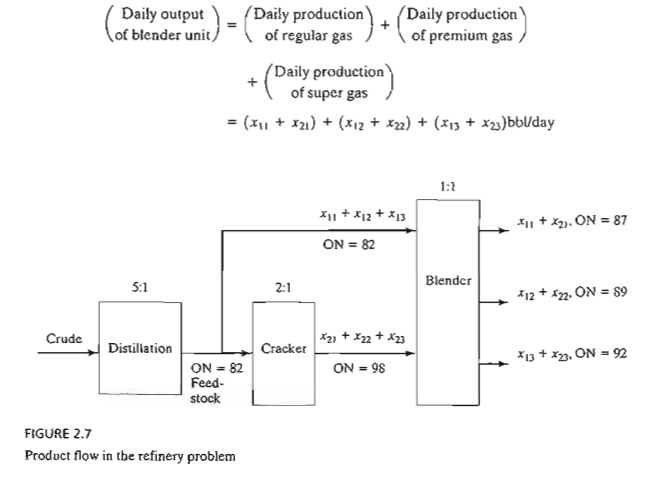
Mathematical Model: Figure 2.7 summarizes the elements of the model. The variables can be defined in terms of two input streams to the blender (feedstock and cracker gasoline) and the three final products. Let

xij = bbl/day of input stream i used to blend final product j, i = 1,2; j  = 1,2,3

Using this definition, we have

Daily production of regular gasoline = x₁₁  + x₂₁  bbl/day

 Daily production of premium gasoline = x₁₂  + x₂₂  bbl/day

Daily production of super gasoline = x₁₃ + x₂₃  bbl/day

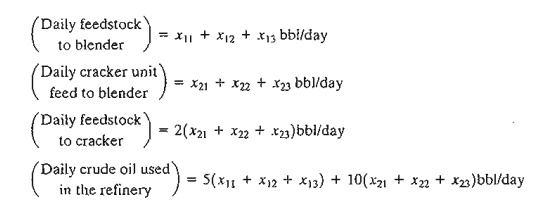
The objective of the model is to maximize the total profit resulting from the sale of all three grades of gasoline. From the definitions given above, we get

The octane number of a gasoline product is the weighted average of the octane numbers of the input streams used in the blending process and can be computed as

The complete model is thus summarized as

Maximize z = 6.70(x₁₁  + x₂₁  + 7.20(x_l2 + x₂₂)  + 8.10(x_l3 + x₂₃)

subject to

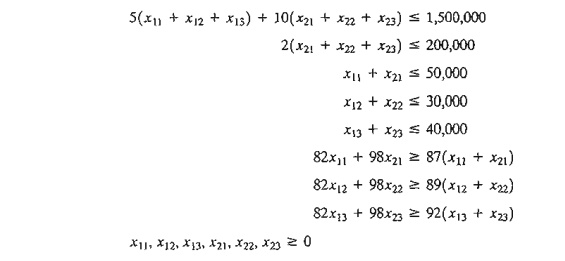
The last three constraints can be simplified to produce a constant right-hand side.

Solution:

The optimum solution (using file amplEx2.3-7.txt) is z = 1,482,000, x₁₁ = 20,625, x₂₁ == 9375, x_I2 =' 16,875, x₂₂ = 13,125, x₁₃ = 15,000, x₂₃ = 25,000. This translates to

Daily profit = $1,482,000

Daily amount of regular gasoline =  x₁₁  + x₂₁  = 20,625 + 9375 = 30,000 bbl/day

Daily amount of premium gasoline =  x₁₂ + x₂₂ = 16,875 + 13,125 = 30,000 bbl/day

Daily amount of regular gasoline =  x_I3  + x₂₃ =  15,000 + 25,000 = 40,000 bbl/day

The solution shows that regular gasoline production is 20,000 bbVday short of satisfying the maximum demand. The demand for the remaining two grades is satisfied.

PROBLEM SET 2.3E

 Hi-V produces three types of canned juice drinks, A, B, and C, using fresh strawberries, grapes, and apples. The daily supply is limited to 200 tons of strawberries, 100 tons of grapes, and 150 tons of apples. The cost per ton of strawberries, grapes, and apples is $200, $100, and $90, respectively. Each ton makes 1500 Ib of strawberry juice, 1200 Ib of grape juice, and 1000 Ib of apple juice. Drink A is a 1:1 mix of strawberry and apple juice. Drink B is 1:1:2 mix of strawberry, grape, and apple juice. Drink C is a 2:3 mix of grape and apple juice. All drinks are canned in 16-oz (1 lb) cans. The price per can is $1.15, $1.25, and $1.20 for drinks A, B, and C. Determine the optimal production mix of the three drinks.

*2. A hardware store packages handyman bags of screws, bolts, nuts, and washers. Screws come in 100-lb boxes and cost $110 each, bolts come in 100-lb boxes and cost $150 each, nuts come in 80-lb boxes and cost $70 each, and washers come in 30-lb boxes and cost $20 each. The handyman package weighs at least lib and must include, by weight, at least 10% screws and 25% bolts, and at most 15% nuts and 10% washers. To balance the package, the number of bolts cannot exceed the number of nuts or the number of washers. A bolt weighs 10 times as much as a nut and 50 times as much as a washer. Determine the optimal mix of the package.

3. All-Natural Coop makes three breakfast cereals, A, B, and C, from four ingredients: rolled oats, raisins, shredded coconuts, and slivered almonds. The daily availabilities of the ingredients are 5 tons, 2 tons, 1 ton, and 1 ton, respectively. The corresponding costs per ton are $100, $120, $110, and $200. Cereal A is a 50:5:2 mix of oats, raisins, and almond. Cereal B is a 60:2:3 mix of oats, coconut, and almond. Cereal C is a 60:3:4:2 mix of oats, raisins, coconut, and almond. The cereals are produced in jumbo 5-lb sizes. All-Natural sells A, B, and Cat $2, $2.50, and $3.00 per box, respectively. The minimum daily demand for cereals A, B, and Cis 500,600, and 500 boxes. Determine the optimal production mix of the cereals and the associated amounts of ingredients.

4. A refinery manufactures two grades of jet fuel, F1 and F2, by blending four types of gaso-line, A, B, C, and D. Fuel F1 uses gasolines A, B, C, and D in the ratio 1:1:2:4, and fuel F2 uses the ratio 2:2:1:3. The supply limits for A, B, C, and Dare 1000, 1200,900, and 1500 bbl/day, respectively. The costs per bbl for gasolines A, B, C, and Dare $120, $90, $100, and $150, respectively. Fuels F1 and F2 sell for $200 and $250 per bbi. The minimum demand for F1 and F2 is 200 and 400 bbUday. Determine the optimal production mix for F1 and F2.

5. An oil company distills two types of crude oil, A and B, to produce regular and premium gasoline and jet fuel. There are limits on the daily availability of crude oil and the minimum demand for the final products. If the production is not sufficient to cover demand, the short-age must be made up from outside sources at a penalty. Surplus production will not be sold immediately and will incur storage cost. The following table provides the data of the situation:

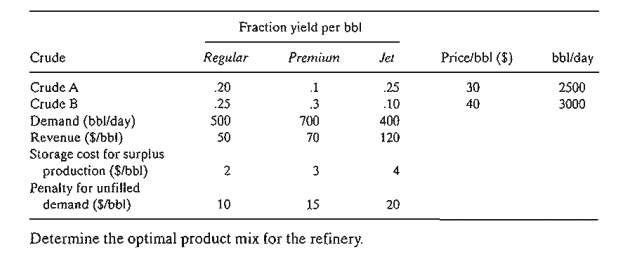
Determine the optimal product mix for the refinery.

6. In the refinery situation of Problem 5, suppose that the distillation unit actually produces the intermediate products naphtha and light oil. One bbl of crude A produces .35 bbl of naphtha and .6 bbl of light oil, and one bbl of crude B produces .45 bbl of naphtha and .5 bbl of light oil. Naphtha and light oil are blended to produce the three final gasoline products: One bbl of regular gasoline has a blend ratio of 2:1 (naphtha to light oil), one bbl of premium gasoline has a blend ratio of ratio of 1:1, and one bbl of jet fuel has a blend ratio of 1:2. Determine the optimal production mix.

7. Hawaii Sugar Company produces brown sugar, processed (white) sugar, powdered sugar, and molasses from sugar cane syrup. The company purchases 4000 tons of syrup weekly and is contracted to deliver at least 25 tons weekly of each type of sugar. The production process starts by manufacturing brown sugar and molasses from the syrup. A ton of syrup produces .3 ton of brown sugar and .1 ton of molasses. White sugar is produced by processing brown sugar. It takes 1 ton of brown sugar to produce .8 ton of white sugar. Powdered sugar is produced from white sugar through a special grinding process that has a 95% conversion efficiency (1 ton of white sugar produces .95 ton of powdered sugar). The profits per ton for brown sugar, white sugar, powdered sugar, and molasses are $150, $200, $230, and $35, respectively. Formulate the problem as a linear program, and deter-mine the weekly production schedule.

8. Shale Oil refinery blends two petroleum stocks,A and B, to produce two high-octane gasoline products, I and II. Stocks A and B are produced at the maximum rates of 450 and 700 bbl/hour, respectively. The corresponding octane numbers are 98 and 89, and the vapor pres-sures are 10 and 8 Ib/in². Gasoline I and gasoline II must have octane numbers of at least 91 and 93, respectively. The vapor pressure associated with both products should not exceed 12 Ib/in². The profits per bbl of I and II are $7 and $10, respectively. Determine the optimum production rate for I and II and their blend ratios from stocks A and B. (Hint: Vapor pressure, like the octane number, is the weighted average of the vapor pressures of the blended stocks.)

9. A foundry smelts steel, aluminum, and cast iron scraps to produce two types of metal ingots, I and II, with specific limits on the aluminum, graphite and silicon contents. Aluminum and silicon briquettes may be used in the smelting process to meet the desired   specifications. The following tables set the specifications of the problem:    

10. Two alloys, A and B, are made from four metals, I, II, III, and IV, according to the following specifications:

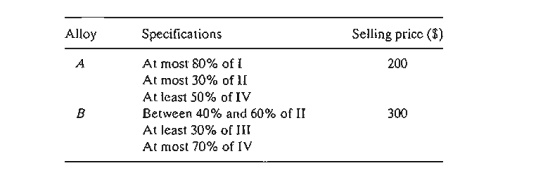
The four metals, in turn, are extracted from three ores according to the following data: 

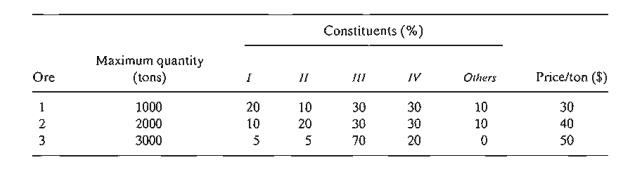
How much of each type of alloy should be produced? (Hint: Let x_kj be tons of are i allocated to alloy k, and define w_k as tons of alloy k produced.)