Water exchange rate - Aquaculture Engineering

Water exchange rate

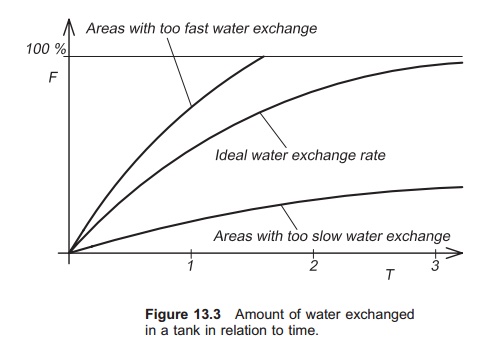
The water exchange rate indicates how quickly the water in closed units is exchanged. This can be defined as the period for which a specific water mole-cule stays in the unit before leaving via the outlet (Fig. 13.3). As the new incoming water will be mixed with the ‘old’ water in the tank, the outlet water will always contain both new and old water. It is important to realize this, and means that if one tank volume is run into a tank full of old water, only part of the old water is exchanged, not all. To describe this, the term ideal water exchange is used. When expecting ideal water exchange and adding 1 l of new water to 100 l of old water, the new and old water will be mixed immediately; for example, the addition of 1 l red water to 100 l of clear water instantly results in pink water. This is a simplification, but it helps us to understand better what is happening with the water exchange, and does not require difficult equations.

Mathematically, the water exchange rate can be calculated as follows (based on developing a differential equation):

F =(1−e^−t/th)×100

where:

t =time after start of filling water into the unitth= time necessary to fill one tank volume at the actual water flow rate; also known as the the-oretical retention time

1.F = water exchange rate (proportion of the water volume in the unit that is exchanged after time t)

Example

Fifty litres of new water is added to a tank that con-tains 100 l water, described as old water, over a period of 5 minutes (i.e. 10 l/min). The same amount of old water flows out through the outlet because the water volume and level are constant. How much of the water volume is exchanged after 5 and 10 min, respectively?

Setting t = 5 min

th= 100 l/(10 l/min) = 10 min

= (1 − e^−5/10) × 100

= (1 – 0.605) × 100

=39.5%

Setting t = 10 min

F  =63.2%

This means that by adding a water volume equal to the tank volume only 63.2% of the water is exchanged, not all as might be expected, the reason being that new and old water are mixed.