Voltage References

Voltage References

The circuit that is primarily designed for providing a constant voltage independent of changes in temperature is called a voltage reference. The most important characteristic of a voltage reference is the temperature coefficient of the output₌ reference voltage Tc_R , and it is expressed as

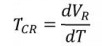
The desirable properties of a voltage reference are:

1.        Reference voltage must be independent of any temperature change.

2.        Reference voltage must have good power supply rejection which is as independent of the supply voltage as possible and

3.        Output voltage must be as independent of the loading of output current as possible, or in other words, the circuit should have low output impedance.

The voltage reference circuit is used to bias the voltage source circuit, and the combination can be called as the voltage regulator. The basic design strategy is producing a zero TCR at a given temperature, and thereby achieving good thermal ability. Temperature stability of the order of 100ppm/⁰ C is typically expected.

Voltage Reference circuit using temperature compensation scheme

The voltage reference circuit using basic temperature compensation scheme is shown below. This design utilizes the close thermal coupling achievable among the monolithic components and this technique compensates the known thermal drifts by introducing an opposing and compensating drift source of equal magnitude.

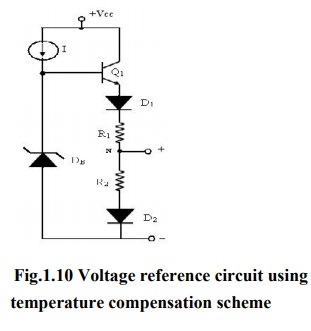
A constant current I is supplied to the avalanche diode D_B and it provides a bias voltage of V_B to the base of Q₁. The temperature dependence of the V_BE drop across Q₁ and those across D₁ and D₂ results in respective temperature coefficients. Hence, with the use of resistors R₁ and R₂ with tapping across them at point N compensates for the temperature drifts in the base-emitter loop of Q₁. This results in generating a voltage reference V_R with normally zero temperature coefficient.

Voltage Reference circuit using Avalanche Diode Reference:

A voltage reference can be implemented using the breakdown phenomenon condition of a heavily doped PN junction. The Zener breakdown is the main mechanism for junctions, which breakdown at a voltage of 5V or less. For integrated transistors, the base-emitter breakdown voltage falls in the range of 6 to 8V. Therefore, the breakdown in the junctions of the integrated transistor is primarily due to avalanche multiplication. The avalanche breakdown voltage VB of a transistor incurs a positive temperature coefficient, typically in the range of 2mV/0 C to 5mV/0 C.

Figure depicts a current reference circuit using avalanche diode reference. The base bias for transistor Q₁ is provided through register R₁ and it also provides the dc current needed to bias DB, D₁ and D₂ . The voltage at the base of Q₁ is equal to the Zener voltage V_B added with two diode drops due to D₁ and D₂. The voltage across R₂ is equal to the voltage at the base of Q₁ less the sum of the base – emitter voltages of Q₁ and Q₂.

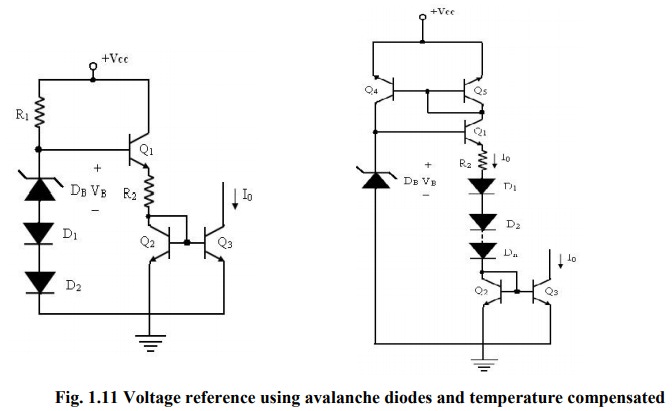
Hence, the voltage across R₂ is approximately equal to that across D_B = V_B. Since Q₂ and Q₃ act as a current mirror circuit, current I₀ equals the current through R₂.

I0 = VB/R2 

It shows that, the output current I₀ has low temperature coefficient, if the temperature coefficient of R₂ is low, such as that produced by a diffused resistor in IC fabrication.

The zero temperature coefficients for output current can be achieved, if diodes are added in series with R₂, so that they can compensate for the temperature variation of R₂ and V_B. The temperature compensated avalanche diode reference source circuit is shown in figure. The transistor Q₄ and Q₅ form an active load current mirror circuit. The base voltage of Q₁ is the voltage V_B across Zener D_B.

Then, V_B = (V_BE * n) +V_BE across Q₁ + V_BE across Q₂ + drop across R₂. Here, n is the number of diodes.

It can be expressed as V_B = ( n+ 2) V_BE - I₀ * R₂

Differentiating for V_B, I₀, R₂ and V_BE +partially,2 with  respect to temperature T, we get

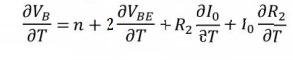
Dividing throughout by I₀  R₂ , we get

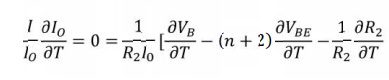
Therefore, zero temperature coefficient of I₀ can be obtained, if the above condition is satisfied.