AC Characteristics of Operational Amplifiers

AC Characteristics:

For small signal sinusoidal (AC) application one has to know the ac characteristics such as frequency response and slew-rate.

1. Frequency Response:

The variation in operating frequency will cause variations in gain magnitude and its phase angle. The manner in which the gain of the op-amp responds to different frequencies is called the frequency response. Op-amp should have an infinite bandwidth BW =∞ (i.e.) if its open loop gain in 90dB with dc signal its gain should remain the same 90 dB through audio and onto high radio frequency. The op-amp gain decreases (roll-off) at higher frequency what reasons to decrease gain after a certain frequency reached. 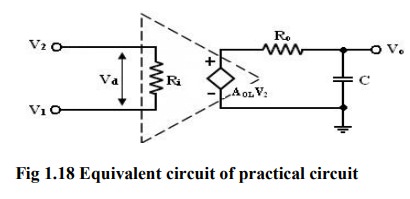There must be a capacitive component in the equivalent circuit of the op-amp. For an op-amp with only one break (corner) frequency all the capacitors effects can be represented by a single capacitor C. Below fig is a modified variation of the low frequency model with capacitor C at the output.

There is one pole due to R₀C and one -20dB/decade. The open loop voltage gain of an op-amp with only one corner frequency is obtained from above fig.

f1 is the corner frequency or the upper 3 dB frequency of the op-amp. The magnitude and phase angle of the open loop volt gain are f1 of frequency can be written as, The magnitude and phase angle characteristics:

1.        For frequency f<< f₁ the magnitude of the gain is 20 log AOL in db.

2.        At frequency f = f₁ the gain in 3 dB down from the dc value of AOL in db. This frequency f1 is called corner frequency.

3.        For f>> f₁ the fain roll-off at the rate off -20dB/decade or -6dB/decade.

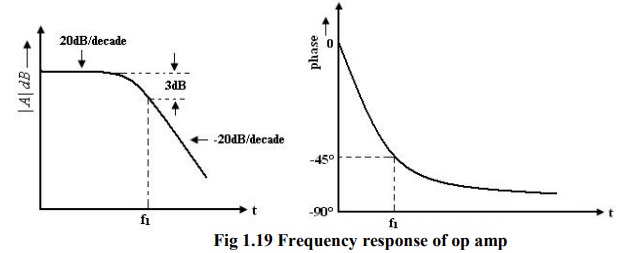
From the phase characteristics that the phase angle is zero at frequency f = 0. At the corner frequency f1 the phase angle is -45º (lagging and an infinite frequency the phase angle is -90 . It shows that a maximum of 90 phase change can occur in an op-amp with a single capacitor C. Zero frequency is taken as the decade below the corner frequency and infinite frequency is one decade above the corner frequency.

2. Circuit Stability:

A circuit or a group of circuit connected together as a system is said to be stable, if its o/p reaches a fixed value in a finite time. A system is said to be unstable, if its o/p increases with time instead of achieving a fixed value. In fact the o/p of an unstable sys keeps on increasing until the system break down. The unstable system is impractical and need be made stable. The criterion gn for stability is used when the system is to be tested practically. In theoretically, always used to test system for stability, ex: Bode plots.

Bode plots are compared of magnitude Vs Frequency and phase angle Vs frequency. Any system whose stability is to be determined can represented by the block diagram.

The block between the output and input is referred to as forward block and the block between the output signal and f/b signal is referred to as feedback block. The content of each block is referred as transfer frequency. From fig. we represented it by AOL (f) which is given by

A_OL (f) = V₀/V_in if V_f = 0 ----- (1)

where A_OL (f) = open loop volt gain.

The closed loop gain A_f is given by A_F = V₀/V_in

= A_OL / (1+(A_OL ) (B)  ----(2)

B = gain of feedback circuit.

B is a constant if the feedback circuit uses only resistive components.

Once the magnitude Vs frequency and phase angle Vs frequency plots are drawn, system stability may be determined as follows

1. Method 1:

Determine the phase angle when the magnitude of (AOL) (B) is 0dB (or) 1.

If phase angle is >-180, the system is stable. However, the some systems the magnitude may never be 0, in that cases method 2, must be used.

2. Method 2:

Determine the phase angle when the magnitude of (AOL) (B) is 0dB (or) 1.

If phase angle is > - 180, If the magnitude is –ve decibels then the system is stable. However, the some systems the phase angle of a system may reach -1800, under such conditions method 1 must be used to determine the system stability.

3. DC Characteristics of op-amp:

Current is taken from the source into the op-amp inputs respond differently to current and

voltage due to mismatch in transistor.

DC output voltages are,

·           Input bias current

·           Input offset current

·           Input offset voltage

·           Thermal drift

Input bias current:

The op-amp‘s input is differential amplifier, which may be made of BJT or FET.

In an ideal op-amp, we assumed that no current is drawn from the input terminals the base currents entering into the inverting and non-inverting terminals (I_B- & I_B+ respectively).

Even though both the transistors are identical, I_B- and I_B+ are not exactly equal due to internal imbalance between the two inputs. Manufacturers specify the input bias current I_B

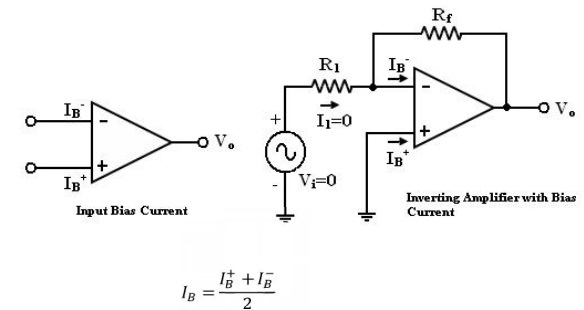
If input voltage V_i = 0V. The output Voltage Vo should also be (V_o = 0) but for I_B = 500nA We find that the output voltage is offset by Op-amp with a 1M feedback resistor

Vo = 500nA X 1M = 500mV

The output is driven to 500mV with zero input, because of the bias currents.

In application where the signal levels are measured in mV, this is totally unacceptable. This can be compensated by a compensation resistor R_comp has been added between the non-inverting input terminal and ground as shown in the figure below.

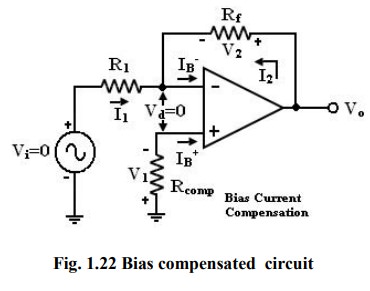
Current I_B⁺ flowing through the compensating resistor R_comp, then by KVL we get,

- V₁+0+V₂-V_o = 0 (or)

V_o = V₂ –  V₁        --------- (1)

By selecting proper value of R_comp, V₂ can be cancelled with V₁ and the V_o = 0. The value of Rcomp is derived as

V₁ = I_B⁺R_comp         (or)

I_B⁺ = V₁/R_comp ------------------------ (2)

The node ‘a’ is at voltage (-V₁). Because the voltage at the non-inverting input terminal is (-V₁). So with V_i = 0 we get,

I₁ = V₁/R₁ ------------------------ (3)

I₂ = V₂/R_f ------------------------ (4)

For compensation, V_o should equal to zero (V_o = 0, V_i = 0). i.e. from equation (3) V₂ = V₁. So that,

I₂ = V₁/R_f ——> (5)

KCL at node ‘a’ gives,

I_B^- = I₂ + I₁ =( V₁/R_f ) +(V₁/R₁) = V₁(R₁+R_f)/R₁R_f  ------------------------ (5)

Assume I_B^- = I_B⁺ and using equation (2) & (5) we get

V₁ (R₁+R_f)/R₁R_f  = V₁/R_comp

R_comp = R₁ || R_f                         ------------------------ (6)

i.e. to compensate for bias current, the compensating resistor, Rcomp should be equal to the parallel combination of resistor R₁ and R_f.

Input offset current:

ü        Bias current compensation will work if both bias currents I_B⁺ and I_B^- are equal.

ü        Since the input transistor cannot be made identical. There will always be some small

difference between I_B⁺ and I_B^-. This difference is called the offset current

|Ios| = I_B⁺-I_B^------------------------- (7)

Offset current I_os for BJT op-amp is 200nA and for FET op-amp is 10pA. Even with bias current compensation, offset current will produce an output voltage when V_i = 0.

Again V₀ = I₂ R_f – V₁

Vo = I₂ R_f - I_B⁺ R_comp

Vo = 1M Ω X 200nA

Vo = 200mV with V_i = 0

Equation (16) the offset current can be minimized by keeping feedback resistance small.

·           Unfortunately to obtain high input impedance, R1 must be kept large.

·           R1 large, the feedback resistor Rf must also be high. So as to obtain reasonable gain.

The T-feedback network is a good solution. This will allow large feedback resistance, while keeping the resistance to ground low (in dotted line).

·           The T-network provides a feedback signal as if the network were a single feedback resistor.

By T to Π conversion,   

To design T- network first pick Rt<<Rf/2 and=calculate

Input offset voltage:

In spite of the use of the above compensating techniques, it is found that the output voltage may still not be zero with zero input voltage [Vo ≠ 0 with Vi= 0]. This is due to unavoidable imbalances inside the op-amp and one may have to apply a small voltage at the input terminal to make output (Vo) = 0.

This voltage is called input offset voltage Vos. This is the voltage required to be applied at the input for making output voltage to zero (Vo = 0).

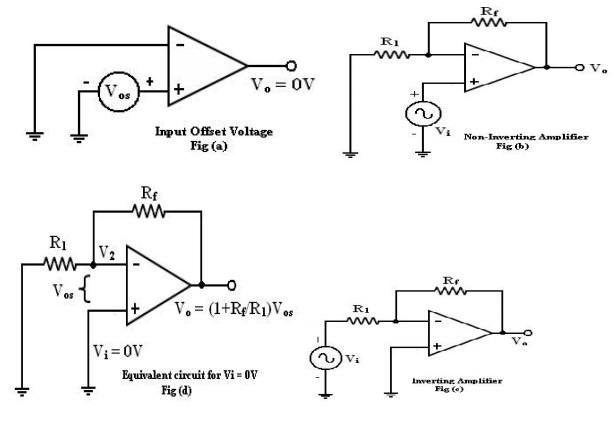
Let us determine the Vos on the output of inverting and non-inverting amplifier. If V_i = 0 (Fig (b) and (c)) become the same as in figure (d).

Total output offset voltage:

The total output offset voltage V_OT could be either more or less than the offset voltage produced at the output due to input bias current (I_B) or input offset voltage alone(V_os). This is because IB and Vos could be either positive or negative with respect to ground. Therefore the maximum offset voltage at the output of an inverting and non-inverting amplifier (figure b, c) without any compensation technique used is given by many op amps provide offset compensation pins to nullify the offset voltage. A 10K potentiometer is placed across offset null pins 1&5. The wipes connected to the negative supply at pin 4. The position of the wipes is adjusted to nullify the offset voltage.

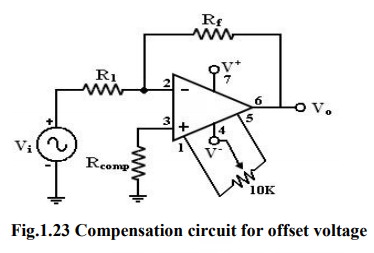
When the given (below) op-amps does not have these offset null pins, external balancing techniques are used.

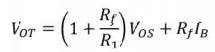
With Rcomp, the total output offset

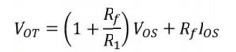
Balancing circuit: Inverting amplifier:

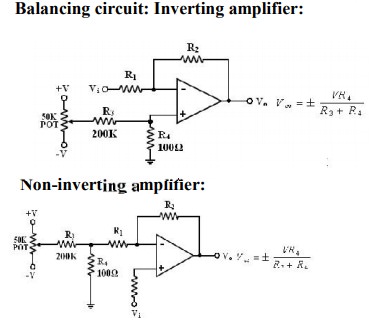
Non-inverting amplifier: 

Thermal drift:

Bias current, offset current, and offset voltage change with temperature. A circuit carefully nulled at 25ºC may not remain. So when the temperature rises to 35ºC. This is called drift. Offset current drift is expressed in nA/ºC. These indicate the change in offset for each degree Celsius change in temperature.