Closed loop op-amp configuration

Closed – loop op-amp configuration:

The op-amp can be effectively utilized in linear applications by providing a feedback from the output to the input, either directly or through another network. If the signal feedback is out- of-phase by 1800 with respect to the input, then the feedback is referred to as negative feedback or degenerative feedback. Conversely, if the feedback signal is in phase with that at the input, then the feedback is referred to as positive feedback or regenerative feedback.

An op – amp that uses feedback is called a closed – loop amplifier. The most commonly used closed – loop amplifier configurations are 1. Inverting amplifier (Voltage shunt amplifier) 2. Non- Inverting amplifier (Voltage – series Amplifier)

Inverting Amplifier:

The inverting amplifier is shown in figure and its alternate circuit arrangement is shown in figure, with the circuit redrawn in a different way to illustrate how the voltage shunt feedback is achieved. The input signal drives the inverting input of the op – amp through resistor R1.

The op – amp has an open – loop gain of A, so that the output signal is much larger than the error voltage. Because of the phase inversion, the output signal is 1800 out – of – phase with the input signal. This means that the feedback signal opposes the input signal and the feedback is negative or degenerative.

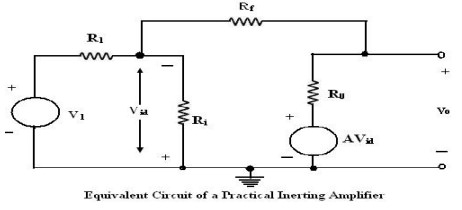
Practical Inverting amplifier:

The practical inverting amplifier has finite value of input resistance and input current, its open voltage gain A₀ is less than infinity and its output resistance R₀ is not zero, as against the ideal inverting amplifier with finite input resistance, infinite open – loop voltage gain and zero output resistance respectively.

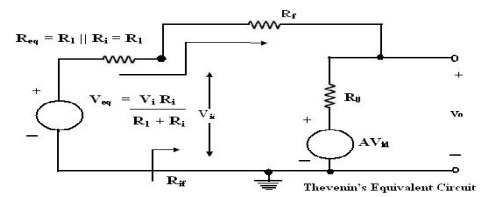
Figure shows the low frequency equivalent circuit model of a practical inverting amplifier. This circuit can be simplified using the Thevenin‘s equivalent circuit shown in figure. The signal source Vi and the resistors R₁ and Ri are replaced by their Thevenin‘s equivalent values. The closed – loop gain AV and the input impedance Rif are calculated as follows.

The input impedance of the op- amp is normally much larger than the input resistance R₁.

Therefore, we can assume V_eq ≈ V_i  and R_eq ≈ R₁ . From the  figure

V₀ = IR₀ = AV_id

V_id= IR_f = AV_id

V₀ = IR₀ = AV_id

Substituting the0 valuef of I derived from above eqn. and obtaining the closed loop gain. It can be observed from above eqn. that when A>> 1, R0 is negligibly small and the product AR₁ >> R₀ +R_f , the closed loop gain is given by   

Av = − R_f/R₁

Which as the same form as given in above eqn for an ideal inverter.

Input Resistance:

R_if = V_id/ I₁ =(R_f+R₀)/(1+A)

Output Resistance:

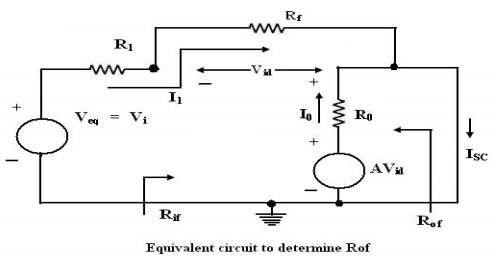
Figure shows the equivalent circuit to determine R_of. The output impedance R_of without the load resistance factor RL is calculated from the open circuit output voltage V_oc and the short circuit output current I_SC.

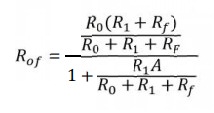
Non –Inverting Amplifier:

The non – inverting Amplifier with negative feedback is shown in figure. The input signal drives the non – inverting input of op-amp. The op-amp provides an internal gain A. The external resistors R1 and Rf form the feedback voltage divider circuit with an attenuation factor of β.

Since the feedback voltage is at the inverting input, it opposes the input voltage at the non – inverting input terminals, and hence the feedback is negative or degenerative.

The differential voltage V_id at the input of the op-amp is zero, because node A is at the same voltage as that of the non- inverting input terminal. As shown in figure, R_f and R₁ form a potential divider. Therefore,

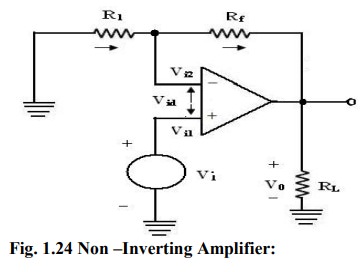
Closed Loop Non – Inverting Amplifier

The input resistance of the op – amp is extremely large (approximately infinity,) since the op – amp draws negligible current from the input signal.

Practical Non –inverting amplifier:

The equivalent circuit of a non- inverting amplifier using the low frequency model is shown below in figure. Using Kirchhoff’s current law at node a,

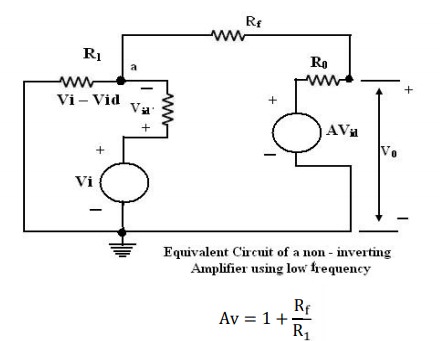
The difference volt is equal to the input volt minus the f/b volt. (or) The feedback volt always opposes the input volt (or out of phase by 1800 with respect to the input voltage) hence the feedback is said to be negative.

It will be performed by computing

1.   Closed loop volt gain

2.   Input and output resistance

3.   Bandwidth

1. Closed loop volt gain:

The closed loop volt gain is A_F = V₀ /V_in

V₀ = A_vid =A(V₁ –V₂ )

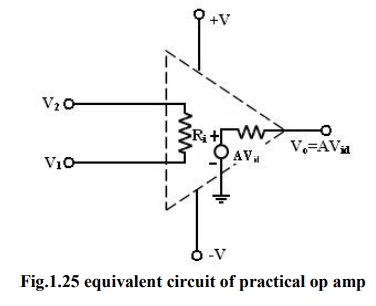
A = large signal voltage gain.

From the above eqn.     

V₀ = A(V₁ – V₂ )