Vector Product and Properties of Vector Product

Vector Product

To define vector product between two vectors, we need the concept of right handed and left handed system.

If we align the fingers of our right hand along the vector and bend our fingers around in the direction of rotation from towards (through an angle  less than 180º ), our thumb will point in the direction of × . Now, following the right-hand rule, × will point in the direction opposite to × (See Fig. 8.38).

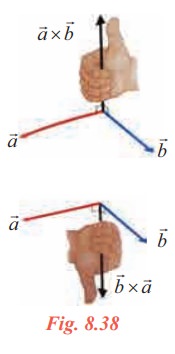
We may also say that if is rotated into the direction of through the angle θ(<π) , then × advances in the same direction as a right-handed screw would if turned in the same way.

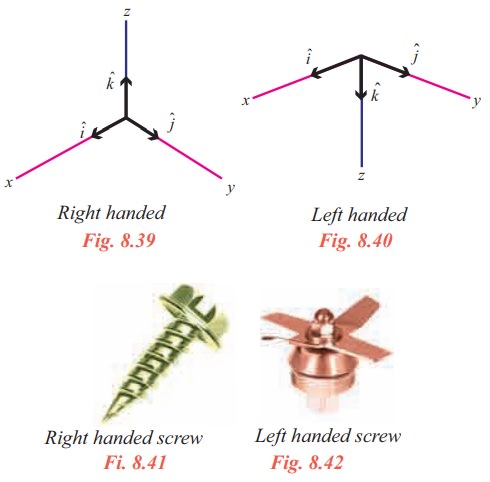
A Cartesian coordinate system is called right-handed if the corresponding unit vectors iˆ, ˆj , kˆ in the positive direction of the axes form a right-handed triple as in Fig. 8.39. The system is called left handed if the sense of kˆ is reversed as in Fig 8.40.

Definition 8.17

Vector product of any two non-zero vectors and is written as × and is defined as

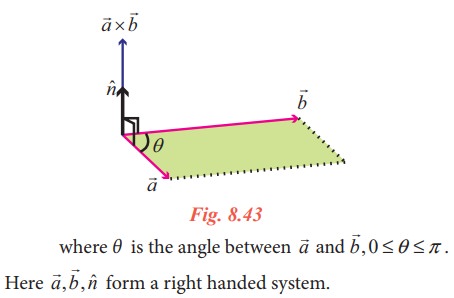
The resultant is a vector with magnitude | || | sinθ and has the direction nˆ.

Further x is a vector perpendicular to both and . That is, x is normal to the plane containing and .

Note 8.6

(i) Note that the order of the vectors is very important to decide the direction of nˆ .

(ii) Since the resultant is a vector, this product is named as vector product. Again, we use the symbol cross ‘×’ to define such a product and hence it has another name cross product.

Geometrical interpretation of vector product

Construct a parallelogram OACB with = and = as adjacent sides.

Let ∟AOB = θ

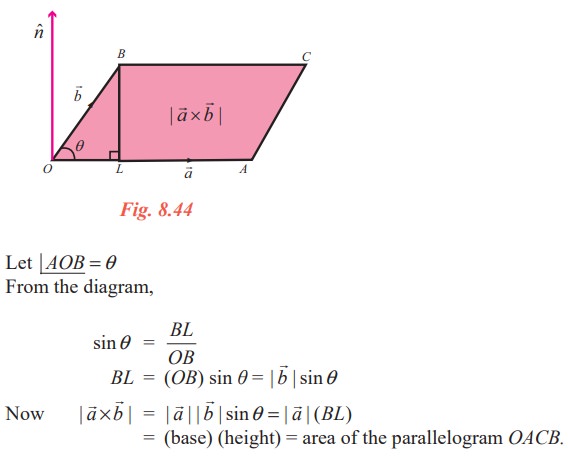
Thus, × is a vector whose magnitude is the area of the parallelogram, having and as its adjacent sides and whose direction nˆ is perpendicular to the plane containing and such that ,, nˆ form a right handed system.

Thus, | × | = area of the parallelogram whose adjacent sides are and .

From the area of the parallelogram, we can deduct the area of the triangle OAC as half of the area of OACB.

Deduction

The area of any triangle whose two sides are and = 1/2 | × |

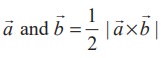
Properties

(i)  Vector product is non-commutative

By definition

Thus vector product is non-commutative.

(ii) If two vectors are collinear or parallel then × = 0 (how?)

But or or × = 0 ⇒ = 0 = 0 and are parallel.

(iii) For any two non-zero vectors and b , × b = ⇔ and are parallel.

Deduction

x=

(iv) With usual meaning of iˆ , jˆ and kˆ (they form a right handed system), the following results are obtained.

It is clear that,

iˆ × iˆ = jˆ × jˆ = kˆ × kˆ =

iˆ × jˆ = kˆ

jˆ × kˆ = iˆ ;

kˆ × iˆ = jˆ

jˆ × iˆ = −kˆ ;

kˆ × jˆ = −iˆ

iˆ × kˆ = − jˆ (how?)

Note 8.7

In this case θ is always acute. Thus, if we try to find the angle using vector product, we get only the acute angle. Hence in problems of finding the angle, the use of dot product is preferable since it specifies the position of the angle θ .

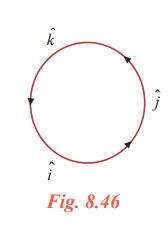
(x) The unit vectors perpendicular to both and  are

Vectors of magnitude λ, perpendicular to both and are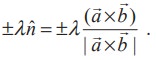

Note 8.8

Instead of and , one can take any two sides.

EXERCISE 8.4