Product of Vectors

Product of Vectors

We have seen the notion of addition of two vectors, subtraction of one vector from another vector and the multiplication of a vector by a scalar. Now we study the notion of product of two vectors. There are two ways of multiplying two vectors.

(i) scalar product (dot product) and

(ii) vector product (cross product).

To define such products we need the angle between two vectors.

Angle between two vectors

Let and be any two vectors represented by and respectively. Angle between and is the angle between their directions when these directions are either both converge as in Fig. 8.36 or both diverge as in Fig. 8.34 from their point of intersection

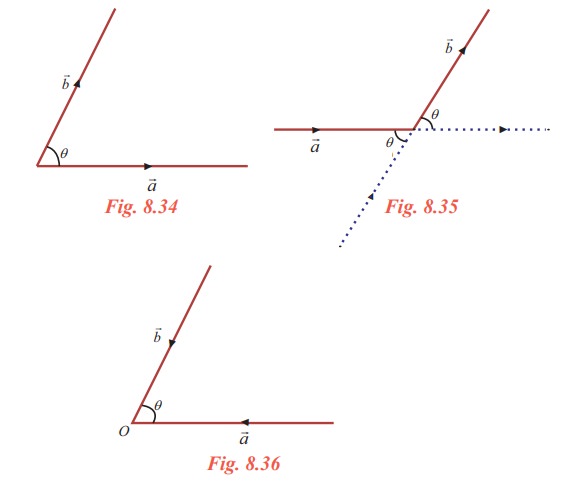
Note that, if q is the angle between two vectors then 0 ≤ θ ≤ π

When θ = 0 or π , the vectors are parallel.

If two vectors neither converge nor diverge as in Fig. 8.35 then we can make them into either converge or diverge by extending the length of the vectors to find the angle between the two vectors.