Direction Cosines and Direction Ratios

Direction Cosines and Direction Ratios

Let P be a point in the space with coordinates (x, y, z) and of distance r from the origin. Let R, S and T be the foots of the perpendiculars drawn from P to the x, y and z axes respectively. Then

∠PRO = ∠PSO = ∠PTO = 90º.

OR = x, OS = y,  OT = z and OP = r.

(It may be difficult to visualize that ∠PRO = ∠PSO = ∠PTO = 90º in the figure; as they are foot of the perpendiculars to the axes from P; in a three dimensional model we can easily visualize the fact.)

Let α, β, γ be the angles made by the vector with the positive x, y and z axes respectively. That is,

∠POR = α , ∠POS = β , and ∠POT = γ .

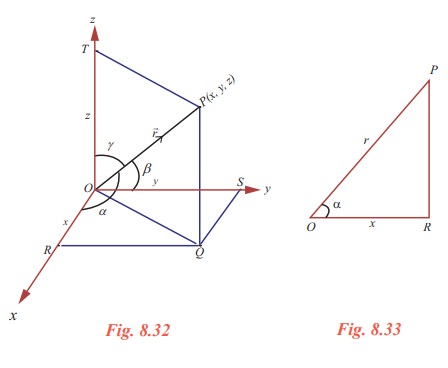
In OPR , ∠PRO = 90°, ∠POR = α ,OR = x , and OP = r. Therefore

cosα = OR/ OP = x /r .

In a similar way we can find that cos β = y/r and cosγ = z/r .

Here the angles α , β , γ are called direction angles of the vector = and cosα ,cos β ,cosγ are called direction cosines of the vector = xiˆ + yˆj + zkˆ. Thus (x/r,y/r,z/r)  where r = √[x + y + z] , are the direction cosines of the vector r = xiˆ + yjˆ + zkˆ .

Any three numbers which are proportional to the direction cosines of vector are called the direction ratios of the vector. Hence the direction ratios of a vector is not unique. For a given vector, we have, infinitely many set of direction ratios.

Observations

(i) For a given non-zero vector, one can find the direction ratios as well as the direction cosines.

(ii) For a given set of direction ratios, one cannot find the corresponding vector.

(iii) For a given set of direction cosines, one cannot find the corresponding vector.

(iv) For a given vector, the triplet of direction cosines is also a triplet of direction ratios.

(v) To find the vector, the magnitude as well as either the set of direction cosines or a set of direction ratios are essential.

Note 8.4

Here we consider a vector whose initial point is at the origin. If the vector whose initial point is not the origin, then, in order to find its direction cosines, we draw a vector with initial point at the origin and parallel to the given vector of same magnitude by translation. By the principle of two equal vectors having the same set of direction cosines, we can find direction cosines of any vector.

Result 8.11

Let = xiˆ + yjˆ + zkˆ  be the position vector of any point and let α , β , γ be the direction angles of . Then

(i) the sum of the squares of the direction cosines of is 1.

(ii) sin2 α + sin2 β + sin2 γ = 2 .

(iii) the direction cosines of

(iv) l, m, n are the direction cosines of a vector if and only if l 2 + m 2 + n2 = 1.

(v) any unit vector can be written as cosα iˆ + cos β ˆj + cosγ kˆ

Proof

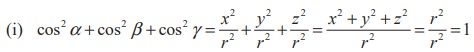
The proofs of (ii), (iii), (iv), and (v) are left as exercise.

Example 8.5

Find a direction ratio and direction cosines of the following vectors.

(i) 3iˆ+4jˆ-6kˆ, (ii) 3iˆ-4kˆ

Solution

Example 8.6

1. (i) Find the direction cosines of a vector whose direction ratios are 2, 3, - 6.

2. (ii) Can a vector have direction angles 30°, 45°,60° ?

(iii) Find the direction cosines of , where A is (2, 3, 1) and B is (3, - 1, 2).

(iv) Find the direction cosines of the line joining (2, 3, 1) and (3, - 1, 2).

(v) The direction ratios of a vector are 2, 3, 6 and it’s magnitude is 5. Find the vector.

Solution

Example 8.7

Show that the points whose position vectors are 2iˆ + 3 jˆ − 5kˆ , 3iˆ + jˆ − 2kˆ and 6iˆ − 5jˆ + 7kˆ are collinear.

Solution

Example 8.8

Find a point whose position vector has magnitude 5 and parallel to the vector 4iˆ - 3 ˆj+10 kˆ.

Solution :

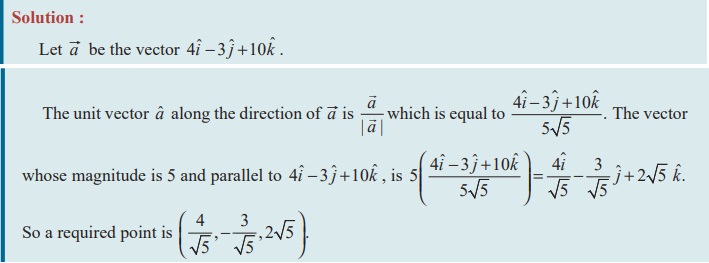
Example 8:9

Prove that the points whose position vectors 2iˆ + 4 jˆ + 3kˆ , 4iˆ + jˆ + 9kˆ and 10iˆ − jˆ + 6kˆ  form a right angled triangle.

Solution

Example 8.10

Show that the vectors  5iˆ + 6 jˆ + 7kˆ, 7iˆ − 8 jˆ + 9kˆ , 3iˆ + 20 jˆ + 5kˆ  are coplanar.

Solution

Let 5iˆ + 6 jˆ + 7kˆ = s(7iˆ − 8 jˆ + 9kˆ) + t (3iˆ + 20 jˆ + 5kˆ)

Equating the components, we have

7s + 3t = 5

-8s + 20t = 6

9s + 5t = 7

Solving first two equations, we get, s = t = 1/2 , which satisfies the third equation.

Thus one vector is a linear combination of other two vectors.

Hence the given vectors are coplanar.

EXERCISE 8.2